
如圖,在 中,已知
中,已知 ,
, 是
是 邊上的一點,
邊上的一點,

(Ⅰ)求 的值;
的值;
(Ⅱ)求 的值。
的值。
(1)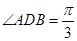 ;(2)
;(2)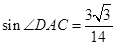 .
.
解析試題分析:本題主要考查解三角形中的正弦定理、余弦定理的應(yīng)用,考查基本的運(yùn)算能力,考查分析問題解決問題的能力.法一:第一問,在 中利用余弦定理求邊
中利用余弦定理求邊 的長,利用
的長,利用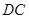 的長度,可以求出
的長度,可以求出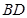 的長,通過
的長,通過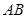 ,
,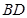 ,角
,角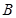 可以判斷出
可以判斷出 為等邊三角形,所以
為等邊三角形,所以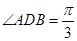 ,
,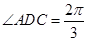 ,
,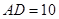 ;第二問,在
;第二問,在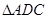 中,利用余弦定理,可以求出
中,利用余弦定理,可以求出 的余弦,再利用平方關(guān)系求出
的余弦,再利用平方關(guān)系求出 ;法二:第一問,在
;法二:第一問,在 中利用正弦定理求出
中利用正弦定理求出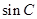 ,從而利用平方關(guān)系求出
,從而利用平方關(guān)系求出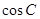 ,在
,在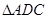 中,利用余弦定理求出
中,利用余弦定理求出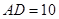 ,再確定
,再確定 為等比三角形,從而得到
為等比三角形,從而得到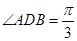 ,
,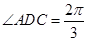 ;第二問,在
;第二問,在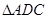 中,再利用正弦定理求出
中,再利用正弦定理求出 的值.
的值.
試題解析:法一:(Ⅰ)由余弦定理
得 ,
,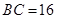 或
或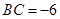 (舍去),
(舍去),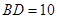 ,
, 為等邊三角形,
為等邊三角形,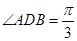 ,
,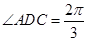 , 8分
, 8分
(Ⅱ) 得
得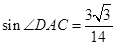 12分
12分
法二:(Ⅰ)由正弦定理可得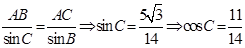
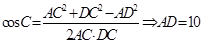 ,
,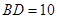 ,
, 為等比三角形,
為等比三角形,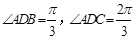 8分
8分
(Ⅱ)由正弦定理可得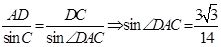 12分
12分
考點:1.余弦定理;2.正弦定理;3.平方關(guān)系.


 津橋教育計算小狀元系列答案
津橋教育計算小狀元系列答案科目:高中數(shù)學(xué) 來源: 題型:解答題
已知函數(shù)f(x)=2 sin xcos x+2cos2x+m在區(qū)間
sin xcos x+2cos2x+m在區(qū)間 上的最大值為2.
上的最大值為2.
(1)求常數(shù)m的值;
(2)在△ABC中,內(nèi)角A,B,C所對的邊分別為a,b,c,若f(A)=1,sin B=3sin C,△ABC的面積為 ,求邊長a.
,求邊長a.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖,制圖工程師要用兩個同中心的邊長均為4的正方形合成一個八角形圖形.由對稱性,圖中8個三角形都是全等的三角形,設(shè) .
.
(1)試用 表示
表示 的面積;
的面積;
(2)求八角形所覆蓋面積的最大值,并指出此時 的大小.
的大小.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
釣魚島及其附屬島嶼是中國固有領(lǐng)土,如圖:點A、B、C分別表示釣魚島、南小島、黃尾嶼,點C在點A的北偏東47°方向,點B在點C的南偏西36°方向,點B在點A的南偏東79°方向,且A、B兩點的距離約為3海里.
(1)求A、C兩點間的距離;(精確到0.01)
(2)某一時刻,我國一漁船在A點處因故障拋錨發(fā)出求救信號.一艘R國艦艇正從點C正東10海里的點P處以18海里/小時的速度接近漁船,其航線為P C
C A(直線行進(jìn)),而我東海某漁政船正位于點A南偏西60°方向20海里的點Q處,收到信號后趕往救助,其航線為先向正北航行8海里至點M處,再折向點A直線航行,航速為22海里/小時.漁政船能否先于R國艦艇趕到進(jìn)行救助?說明理由.
A(直線行進(jìn)),而我東海某漁政船正位于點A南偏西60°方向20海里的點Q處,收到信號后趕往救助,其航線為先向正北航行8海里至點M處,再折向點A直線航行,航速為22海里/小時.漁政船能否先于R國艦艇趕到進(jìn)行救助?說明理由.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com