Question

19．△ABC中，頂點A的坐標為（1，2），高BE，CF所在直線的方程分別為2x-3y+1=0，x+y=0，求這個三角形三條邊所在直線的方程．

Answer 1

分析 由題意求出直線AC、AB的斜率，寫出直線AC、AB的方程；由直線與高線的交點求出C、B的坐標，即可寫出直線BC的方程．

解答 解：畫出圖形如圖所示，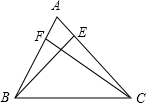
高BE所在直線的方程為2x-3y+1=0，
∴直線AC的斜率為-$\frac{3}{2}$，
又高CF所在直線的方程x+y=0，
∴直線AB的斜率為1；
∴直線AC的方程為3x+2y-7=0，
直線AB的方程為x-y+1=0；
再由$\left\{\begin{array}{l}{3x+2y-7=0}\\{x-y+1=0}\end{array}\right.$，
解得C點坐標為（7，-7）；
由$\left\{\begin{array}{l}{2x-3y+1=0}\\{x-y+1=0}\end{array}\right.$，
解得B點坐標為（-2，-1）；
于是直線BC的方程為$\frac{y+1}{-7+1}$=$\frac{x+2}{7+2}$，
化簡得2x+3y+7=0．

點評 本題考查了直線方程的應用問題，也考查了垂直關系與方程組的解法問題，是中檔題．