
【題目】已知函數![]() .
.
(1)若![]() 是
是![]() 的極大值點,求
的極大值點,求![]() 的值;
的值;
(2)若![]() 在
在![]() 上只有一個零點,求
上只有一個零點,求![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)首先對函數![]() 進行求導,然后通過極大值點所對應的導函數值為0即可求出
進行求導,然后通過極大值點所對應的導函數值為0即可求出![]() 的值,最后通過檢驗即可得出結果;
的值,最后通過檢驗即可得出結果;
(2)首先可以設方程![]() 并寫出方程
并寫出方程![]() 的導函數,然后將
的導函數,然后將![]() 在
在![]() 上只有一個零點轉化為
上只有一個零點轉化為![]() 在
在![]() 上只有一個零點,再利用方程
上只有一個零點,再利用方程![]() 的導函數求出方程
的導函數求出方程![]() 的最小值,最后對方程
的最小值,最后對方程![]() 的最小值與0之間的關系進行分類討論即可得出結果。
的最小值與0之間的關系進行分類討論即可得出結果。
(1)![]() ,
,
因為![]() 是
是![]() 的極大值點,所以
的極大值點,所以![]() ,解得
,解得![]() ,
,
當![]() 時,
時,![]() ,
,![]() ,
,
令![]() ,解得
,解得![]() ,
,
當![]() 時,
時,![]() ,
,![]() 在
在![]() 上單調遞減,又
上單調遞減,又![]() ,
,
所以當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() ,
,
故![]() 是
是![]() 的極大值點;
的極大值點;
(2)令![]() ,
,![]() ,
,
![]() 在
在![]() 上只有一個零點即
上只有一個零點即![]() 在
在![]() 上只有一個零點,
上只有一個零點,
當![]() 時,
時,![]() ,
,![]() 單調遞減;當
單調遞減;當![]() 時,
時,![]() ,
,![]() 單調遞增,所以
單調遞增,所以![]() .
.
(Ⅰ)當![]() ,即
,即![]() 時,
時,![]() 時,
時,![]() 在
在![]() 上只有一個零點,即
上只有一個零點,即![]() 在
在![]() 上只有一個零點.
上只有一個零點.
(Ⅱ)當![]() ,即
,即![]() 時,取
時,取![]() ,
,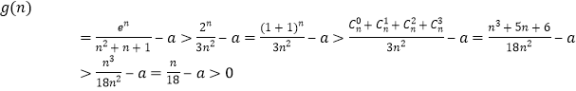 ,
,
①若![]() ,即
,即![]() 時,
時,![]() 在
在![]() 和
和![]() 上各有一個零點,即
上各有一個零點,即![]() 在
在![]() 上有2個零點,不符合題意;
上有2個零點,不符合題意;
②當![]() 即
即![]() 時,
時,![]() 只有在
只有在![]() 上有一個零點,即
上有一個零點,即![]() 在
在![]() 上只有一個零點,
上只有一個零點,
綜上得,當![]() 時,
時,![]() 在
在![]() 上只有一個零點。
上只有一個零點。


科目:高中數學 來源: 題型:
【題目】拋擲一個質地均勻的骰子的試驗,事件A表示“小于5的偶數點出現”,事件B表示“不小于5的點數出現”,則一次試驗中,事件A或事件B至少有一個發生的概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某超市為調查會員某年度上半年的消費情況制作了有獎調查問卷發放給所有會員,并從參與調查的會員中隨機抽取![]() 名了解情況并給予物質獎勵.調查發現抽取的
名了解情況并給予物質獎勵.調查發現抽取的![]() 名會員消費金額(單位:萬元)都在區間
名會員消費金額(單位:萬元)都在區間![]() 內,調查結果按消費金額分成
內,調查結果按消費金額分成![]() 組,制作成如下的頻率分布直方圖.
組,制作成如下的頻率分布直方圖.
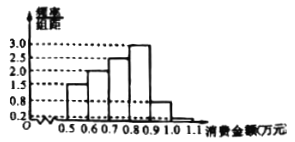
(1)求該![]() 名會員上半年消費金額的平均值與中位數;(以各區間的中點值代表該區間的均值)
名會員上半年消費金額的平均值與中位數;(以各區間的中點值代表該區間的均值)
(2)現采用分層抽樣的方式從前![]() 組中選取
組中選取![]() 人進行消費愛好調查,然后再從前
人進行消費愛好調查,然后再從前![]() 組選取的人中隨機選
組選取的人中隨機選![]() 人,求這
人,求這![]() 人都來自第
人都來自第![]() 組的概率.
組的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知正方體![]() ,過對角線
,過對角線![]() 作平面
作平面![]() 交棱
交棱![]() 于點
于點![]() ,交棱
,交棱![]() 于點
于點![]() ,下列正確的是( )
,下列正確的是( )
A.平面![]() 分正方體所得兩部分的體積相等;
分正方體所得兩部分的體積相等;
B.四邊形![]() 一定是平行四邊形;
一定是平行四邊形;
C.平面![]() 與平面
與平面![]() 不可能垂直;
不可能垂直;
D.四邊形![]() 的面積有最大值.
的面積有最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() 的長軸長為
的長軸長為![]() ,
, ![]() ,
, ![]() 是其長軸頂點,
是其長軸頂點, ![]() 是橢圓上異于
是橢圓上異于![]() ,
, ![]() 的動點,且
的動點,且![]() .
.
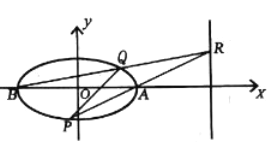
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)如圖,若動點![]() 在直線
在直線![]() 上,直線
上,直線![]() ,
, ![]() 分別交橢圓
分別交橢圓![]() 于
于![]() ,
, ![]() 兩點.請問:直線
兩點.請問:直線![]() 是否過定點?若是,求出定點坐標;若不是,請說明理由.
是否過定點?若是,求出定點坐標;若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (其中
(其中![]() )在點
)在點![]() 處的切線斜率為1.
處的切線斜率為1.
(1)用![]() 表示
表示![]() ;
;
(2)設![]() ,若
,若![]() 對定義域內的
對定義域內的![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍;
的取值范圍;
(3)在(2)的前提下,如果![]() ,證明:
,證明: ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2021年開始,我省將試行“3+1+2“的普通高考新模式,即除語文、數學、外語3門必選科目外,考生再從物理、歷史中選1門,從化學、生物、地理、政治中選2門作為選考科目.為了幫助學生合理選科,某中學將高一每個學生的六門科目綜合成績按比例均縮放成5分制,繪制成雷達圖.甲同學的成績雷達圖如圖所示,下面敘述一定不正確的是( )

A.甲的物理成績領先年級平均分最多
B.甲有2個科目的成績低于年級平均分
C.甲的成績從高到低的前3個科目依次是地理、化學、歷史
D.對甲而言,物理、化學、地理是比較理想的一種選科結果
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com