
【題目】我們國家正處于老齡化社會中,老有所依也是政府的民生工程.某市共有戶籍人口400萬,其中老人(年齡60歲及以上)人數(shù)約有66萬,為了了解老人們的健康狀況,政府從老人中隨機(jī)抽取600人并委托醫(yī)療機(jī)構(gòu)免費(fèi)為他們進(jìn)行健康評估,健康狀況共分為不能自理、不健康尚能自理、基本健康、健康四個等級,并以80歲為界限分成兩個群體進(jìn)行統(tǒng)計,樣本分布被制作成如下圖表:
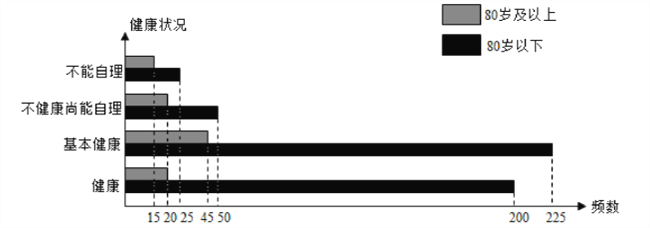
(1)若采用分層抽樣的方法再從樣本中的不能自理的老人中抽取8人進(jìn)一步了解他們的生活狀況,則兩個群體中各應(yīng)抽取多少人?
(2)估算該市80歲及以上長者占全市戶籍人口的百分比;
(3)據(jù)統(tǒng)計該市大約有五分之一的戶籍老人無固定收入,政府計劃為這部分老人每月發(fā)放生活補(bǔ)貼,標(biāo)準(zhǔn)如下:
①80歲及以上長者每人每月發(fā)放生活補(bǔ)貼200元;
②80歲以下老人每人每月發(fā)放生活補(bǔ)貼120元;
③不能自理的老人每人每月額外發(fā)放生活補(bǔ)貼100元.
利用樣本估計總體,試估計政府執(zhí)行此計劃的年度預(yù)算.(單位:億元,結(jié)果保留兩位小數(shù))
【答案】(1)80歲及以上應(yīng)抽取: ![]() 人,80歲以下應(yīng)抽取:
人,80歲以下應(yīng)抽取: ![]() 人;(2)
人;(2) ![]() ;(3)2.22億元.
;(3)2.22億元.
【解析】試題分析:(Ⅰ)從圖表中求出不能自理的80歲及以上長者占比,由此能求出抽取16人中不能自理的80歲及以上長者人數(shù)為.
(Ⅱ)求出在600人中80歲及以上長者在老人中占比,用樣本估計總體,能求出80歲及以上長者占戶籍人口的百分比.
(Ⅲ)用樣本估計總體,設(shè)任一戶籍老人每月享受的生活補(bǔ)助為X元,則Xr可能取值為0,120,200,220,300,分別求出相應(yīng)的概率,由此能求出隨機(jī)變量X的分布列、EX,從而能估計政府執(zhí)行此計劃的年度預(yù)算.
試題解析:
(1)數(shù)據(jù)整理如下表:
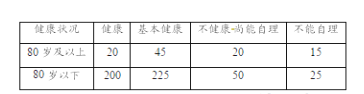
從圖表中知不能自理的![]() 歲及以上長者比為:
歲及以上長者比為: ![]()
故抽取![]() 人中不能自理的
人中不能自理的![]() 歲及以上長者人數(shù)為
歲及以上長者人數(shù)為![]()
![]() 歲以下長者人數(shù)為
歲以下長者人數(shù)為![]() 人
人![]()
(2)在![]() 人中
人中![]() 歲及以上長者在老人中占比為:
歲及以上長者在老人中占比為: ![]()
用樣本估計總體, ![]() 歲及以上長者共有
歲及以上長者共有![]() 萬,
萬,
![]() 歲及以上長者占戶籍人口的百分比為
歲及以上長者占戶籍人口的百分比為![]() %=
%=![]() %,
%,
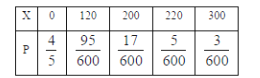
(3)用樣本估計總體,設(shè)任一戶籍老人每月享受的生活補(bǔ)助為![]() 元,
元,
![]()
![]()
則隨機(jī)變量的分布列為:
![]()
全市老人的總預(yù)算為![]() 元,
元,
政府執(zhí)行此計劃的年度預(yù)算約為![]() 億元.
億元.
求解離散型隨機(jī)變量的數(shù)學(xué)期望的一般步驟為:
第一步是“判斷取值”,即判斷隨機(jī)變量的所有可能取值,以及取每個值所表示的意義;
第二步是“探求概率”,即利用排列組合,枚舉法,概率公式(常見的有古典概型公式、幾何概率公式、互斥事件的概率和公式、獨(dú)立事件的概率積,以及對立事件的概率公式等),求出隨機(jī)變量取每個值時的概率;
第三步是“寫分布列”,即按規(guī)范形式寫出分布列,并注意用分布列的性質(zhì)檢驗(yàn)所求的分布列或某事件的概率是否正確;
第四步是“求期望值”,一般利用離散型隨機(jī)變量的數(shù)學(xué)期望的定義求期望的值,對于有些實(shí)際問題中的隨機(jī)變量,如果能夠斷定它服從某常見的典型分布(如二項分布![]() ,則此隨機(jī)變量的期望可直接利用這種典型分布的期望公式(
,則此隨機(jī)變量的期望可直接利用這種典型分布的期望公式(![]() )求得.因此,應(yīng)熟記常見的典型分布的期望公式,可加快解題速度.
)求得.因此,應(yīng)熟記常見的典型分布的期望公式,可加快解題速度.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】以直角坐標(biāo)系的原點(diǎn)O為極點(diǎn),x軸的正半軸為極軸建立極坐標(biāo)系,曲線C的極坐標(biāo)方程為ρsin2α﹣4cosα=0.已知直線l的參數(shù)方程為![]() (
(![]() 為參數(shù)),點(diǎn)M的直角坐標(biāo)為
為參數(shù)),點(diǎn)M的直角坐標(biāo)為![]() .
.
(1)求直線l和曲線C的普通方程;
(2)設(shè)直線l與曲線C交于A,B兩點(diǎn),求![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() :
: ![]() 的長軸長為6,且橢圓
的長軸長為6,且橢圓![]() 與圓
與圓![]() :
: ![]() 的公共弦長為
的公共弦長為![]() .
.
(1)求橢圓![]() 的方程.
的方程.
(2)過點(diǎn)![]() 作斜率為
作斜率為![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于兩點(diǎn)
交于兩點(diǎn)![]() ,
, ![]() ,試判斷在
,試判斷在![]() 軸上是否存在點(diǎn)
軸上是否存在點(diǎn)![]() ,使得
,使得![]() 為以
為以![]() 為底邊的等腰三角形.若存在,求出點(diǎn)
為底邊的等腰三角形.若存在,求出點(diǎn)![]() 的橫坐標(biāo)的取值范圍,若不存在,請說明理由.
的橫坐標(biāo)的取值范圍,若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下列判斷正確的是( )
A.![]() 或
或![]()
B.命題“若![]() 都是偶數(shù),則
都是偶數(shù),則![]() 是偶數(shù)”的逆否命題是“若
是偶數(shù)”的逆否命題是“若![]() 不是偶數(shù),則
不是偶數(shù),則![]() 都不是偶數(shù)”
都不是偶數(shù)”
C.若“![]() 或
或![]() ”為假命題,則“非
”為假命題,則“非![]() 且非
且非![]() ”是真命題
”是真命題
D.已知![]() 是實(shí)數(shù),關(guān)于
是實(shí)數(shù),關(guān)于![]() 的不等式
的不等式![]() 的解集是空集,必有
的解集是空集,必有![]() 且
且![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,且在
,且在![]() 軸上的頂點(diǎn)分別為
軸上的頂點(diǎn)分別為![]() ,
,![]() .
.
(1)求橢圓的方程;
(2)若直線![]() 與
與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]() 為直線
為直線![]() 上異于點(diǎn)
上異于點(diǎn)![]() 的任一點(diǎn),直線
的任一點(diǎn),直線![]() 分別與橢圓交于
分別與橢圓交于![]() 點(diǎn),試問直線
點(diǎn),試問直線![]() 能否通過橢圓的焦點(diǎn)?若能,求出
能否通過橢圓的焦點(diǎn)?若能,求出![]() 的值,若不能,說明理由.
的值,若不能,說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下列有關(guān)命題的說法錯誤的是( )
A. 若“![]() ”為假命題,則p,q均為假命題
”為假命題,則p,q均為假命題
B. “ ![]() ”是“
”是“![]() ”的充分不必要條件
”的充分不必要條件
C. “![]() ”的必要不充分條件是“
”的必要不充分條件是“![]() ”
”
D. 若命題p:![]() ,
,![]() ,則命題
,則命題![]() :
:![]() ,
,![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖所示,已知AB丄平面BCD,M、N分別是AC、AD的中點(diǎn),BC 丄 CD.

(1)求證:MN//平面BCD;
(2)若AB=1,BC=![]() ,求直線AC與平面BCD所成的角.
,求直線AC與平面BCD所成的角.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下列說法錯誤的是( )
A. 命題![]() “
“![]() ”,則
”,則![]() :“
:“![]() ”
”
B. 命題“若![]() ,則
,則![]() ”的否命題是真命題
”的否命題是真命題
C. 若![]() 為假命題,則
為假命題,則![]() 為假命題
為假命題
D. 若![]() 是
是![]() 的充分不必要條件,則
的充分不必要條件,則![]() 是
是![]() 的必要不充分條件
的必要不充分條件
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)當(dāng)![]() 時,求
時,求![]() 在區(qū)間
在區(qū)間![]() 上的最值;
上的最值;
(2)討論函數(shù)![]() 的單調(diào)性;
的單調(diào)性;
(3)當(dāng)![]() 時,有
時,有![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com