
【題目】已知橢圓![]() :
: ![]() 的長軸長為6,且橢圓
的長軸長為6,且橢圓![]() 與圓
與圓![]() :
: ![]() 的公共弦長為
的公共弦長為![]() .
.
(1)求橢圓![]() 的方程.
的方程.
(2)過點![]() 作斜率為
作斜率為![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于兩點
交于兩點![]() ,
, ![]() ,試判斷在
,試判斷在![]() 軸上是否存在點
軸上是否存在點![]() ,使得
,使得![]() 為以
為以![]() 為底邊的等腰三角形.若存在,求出點
為底邊的等腰三角形.若存在,求出點![]() 的橫坐標的取值范圍,若不存在,請說明理由.
的橫坐標的取值范圍,若不存在,請說明理由.
【答案】(1)![]() ;(2)見解析.
;(2)見解析.
【解析】試題分析:(1)由長軸長可得![]() 值,公共弦長恰為圓
值,公共弦長恰為圓![]() 直徑,可知橢圓經過點
直徑,可知橢圓經過點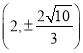 ,利用待定系數法可得橢圓
,利用待定系數法可得橢圓![]() 方程;(2)可令直線
方程;(2)可令直線![]() 的解析式為
的解析式為![]() ,設
,設![]() ,
, ![]() 的中點為
的中點為![]() ,將直線方程與橢圓方程聯立,消去
,將直線方程與橢圓方程聯立,消去![]() ,利用根與系數的關系可得
,利用根與系數的關系可得![]() ,由等腰三角形中
,由等腰三角形中![]() ,可得
,可得![]() ,得出
,得出![]() 中
中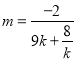 .由此可得
.由此可得![]() 點的橫坐標
點的橫坐標![]() 的范圍.
的范圍.
試題解析:(1)由題意可得![]() ,所以
,所以![]() .由橢圓
.由橢圓![]() 與圓
與圓![]() :
: ![]() 的公共弦長為
的公共弦長為![]() ,恰為圓
,恰為圓![]() 的直徑,可得橢圓
的直徑,可得橢圓![]() 經過點
經過點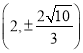 ,所以
,所以![]() ,解得
,解得![]() .所以橢圓
.所以橢圓![]() 的方程為
的方程為![]() .
.
(2)直線![]() 的解析式為
的解析式為![]() ,設
,設![]() ,
, ![]() 的中點為
的中點為![]() .假設存在點
.假設存在點![]() ,使得
,使得![]() 為以
為以![]() 為底邊的等腰三角形,則
為底邊的等腰三角形,則![]() .由
.由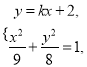 得
得![]() ,故
,故![]() ,所以
,所以![]() ,
, ![]() .因為
.因為![]() ,所以
,所以![]() ,即
,即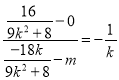 ,所以
,所以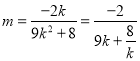 .當
.當![]() 時,
時, ![]() ,所以
,所以![]() ;當
;當![]() 時,
時, ![]() ,所以
,所以![]() .
.
綜上所述,在![]() 軸上存在滿足題目條件的點
軸上存在滿足題目條件的點![]() ,且點
,且點![]() 的橫坐標的取值范圍為
的橫坐標的取值范圍為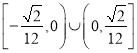 .
.


 暑假作業暑假快樂練西安出版社系列答案
暑假作業暑假快樂練西安出版社系列答案科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,圓C的方程為x2+y2﹣8x+15=0,若直線y=kx﹣2上至少存在一點,使得以該點為圓心,1為半徑的圓與圓C有公共點,則k的最大值是 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知等差數列{an}的前n項和為 ![]() ,且a1與a5的等差中項為18.
,且a1與a5的等差中項為18.
(1)求{an}的通項公式;
(2)若an=2log2bn , 求數列{bn}的前n項和Tn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2017年春節期間,某服裝超市舉辦了一次有獎促銷活動,消費每超過600元(含600元),均可抽獎一次,抽獎方案有兩種,顧客只能選擇其中的一種.
方案一:從裝有10個形狀、大小完全相同的小球(其中紅球3個,黑球7個)的抽獎盒中,一次性摸出3個球,其中獎規則為:若摸到3個紅球,享受免單優惠;若摸出2個紅球則打6折,若摸出1個紅球,則打7折;若沒摸出紅球,則不打折.
方案二:從裝有10個形狀、大小完全相同的小球(其中紅球3個,黑球7個)的抽獎盒中,有放回每次摸取1球,連摸3次,每摸到1次紅球,立減200元.
(1)若兩個顧客均分別消費了600元,且均選擇抽獎方案一,試求兩位顧客均享受免單優惠的概率;
(2)若某顧客消費恰好滿1000元,試從概率的角度比較該顧客選擇哪一種抽獎方案更合算?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=loga(x+2)+loga(3﹣x),其中0<a<1.
(1)求函數f(x)的定義域;
(2)若函數f(x)的最小值為﹣4,求a的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖(1)五邊形![]() 中,
中, ![]()
![]() ,將
,將![]() 沿
沿![]() 折到
折到![]() 的位置,得到四棱錐
的位置,得到四棱錐![]() ,如圖(2),點
,如圖(2),點![]() 為線段
為線段![]() 的中點,且
的中點,且![]() 平面
平面![]() .
.
(1)求證:平面![]() 平面
平面![]() ;
;
(2)若直線![]() 與所成角的正切值為
與所成角的正切值為![]() ,求直線
,求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設f(x)是定義在R上的偶函數,在[0,+∞)上單調遞增.若a=f(log ![]()
![]() ),b=f(log
),b=f(log ![]()
![]() ),c=f(﹣2),則a,b,c的大小關系是( )
),c=f(﹣2),則a,b,c的大小關系是( )
A.a>b>c
B.b>c>a
C.c>b>a
D.c>a>b
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com