
【題目】若函數f(x)在其圖像上存在不同的兩點A(x1 , y1),B(x2 , y2),其坐標滿足條件:|x1x2+y1y2|﹣ ![]() 的最大值為0,則稱f(x)為“柯西函數”, 則下列函數:
的最大值為0,則稱f(x)為“柯西函數”, 則下列函數:
①f(x)=x+ ![]() (x>0);
(x>0);
②f(x)=lnx(0<x<3);
③f(x)=2sinx;
④f(x)= ![]() .
.
其中為“柯西函數”的個數為( )
A.1
B.2
C.3
D.4
【答案】C
【解析】解:由柯西不等式得:對任意實數x1 , y1 , x2 , y2 , |x1x2+y1y2|﹣ ![]() ≤0恒成立(當且僅當存在實數k,使得x1=kx2 , y1=ky2取等號),若函數f(x)在其圖像上存在不同的兩點A(x1 , y1),B(x2 , y2),其坐標滿足條件:|x1x2+y1y2|﹣
≤0恒成立(當且僅當存在實數k,使得x1=kx2 , y1=ky2取等號),若函數f(x)在其圖像上存在不同的兩點A(x1 , y1),B(x2 , y2),其坐標滿足條件:|x1x2+y1y2|﹣ ![]() 的最大值為0,則函數f(x)在其圖像上存在不同的兩點A(x1 , y1),B(x2 , y2),使得
的最大值為0,則函數f(x)在其圖像上存在不同的兩點A(x1 , y1),B(x2 , y2),使得 ![]() 共線,即存在點A、B與點O共線; 對于①,f(x)=x+
共線,即存在點A、B與點O共線; 對于①,f(x)=x+ ![]() (x>0)存在;
(x>0)存在;
對于②,f(x)=lnx ![]() (0<x<3)不存在;
(0<x<3)不存在;
對于③,f(x)=2sinx存在;
對于④,f(x)= ![]() 存在.
存在.
故選:C.
【考點精析】解答此題的關鍵在于理解函數的最值及其幾何意義的相關知識,掌握利用二次函數的性質(配方法)求函數的最大(小)值;利用圖象求函數的最大(小)值;利用函數單調性的判斷函數的最大(小)值.


 心算口算巧算一課一練系列答案
心算口算巧算一課一練系列答案 應用題作業本系列答案
應用題作業本系列答案科目:高中數學 來源: 題型:
【題目】(2015·湖南)某商場舉行有獎促銷活動,顧客購買一定金額商品后即可抽獎,每次抽獎都從裝有4個紅球、6個白球的甲箱和裝有5個紅球、5個白球的乙箱中,各隨機摸出1個球,在摸出的2個球中,若都是紅球,則獲一等獎;若只有1個紅球,則獲二等獎;若沒有紅球,則不獲獎,求下列問題:(1)求顧客抽獎1次能獲獎的概率(2)若某顧客有3次抽獎機會,記該顧客在3次抽獎中獲一等獎的次數為 X ,求 X 的分布列和數學期望.
(1)(1)求顧客抽獎1次能獲獎的概率
(2)(2)若某顧客有3次抽獎機會,記該顧客在3次抽獎中獲一等獎的次數為![]() , 求
, 求![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 在區間
在區間![]() 上的最大值為4,最小值為1.
上的最大值為4,最小值為1.
(1)求實數![]() 、
、![]() 的值;
的值;
(2)記![]() ,若
,若![]() 在
在![]() 上是單調函數,求實數
上是單調函數,求實數![]() 的取值范圍;
的取值范圍;
(3)對于函數![]() ,用
,用![]() ,1,2,
,1,2,![]() ,
,![]() ,
,![]() 將區間
將區間![]() 任意劃分成
任意劃分成![]() 個小區間,若存在常數
個小區間,若存在常數![]() ,使得和式
,使得和式![]() 對任意的劃分恒成立,則稱函數
對任意的劃分恒成立,則稱函數![]() 為
為![]() 上的有界變差函數.記
上的有界變差函數.記![]() ,試判斷函數
,試判斷函數![]() 是否為在
是否為在![]() 上的有界變差函數?若是,求
上的有界變差函數?若是,求![]() 的最小值;若不是,請說明理由.
的最小值;若不是,請說明理由.
(參考公式:![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系中 ![]() 中,已知曲線
中,已知曲線 ![]() 經過點
經過點 ![]() ,其參數方程為
,其參數方程為 ![]() (
( ![]() 為參數),以原點
為參數),以原點 ![]() 為極點,
為極點, ![]() 軸的正半軸為極軸建立極坐標系.
軸的正半軸為極軸建立極坐標系.
(1)求曲線 ![]() 的極坐標方程;
的極坐標方程;
(2)若直線 ![]() 交
交 ![]() 于點
于點 ![]() ,且
,且 ![]() ,求證:
,求證: ![]() 為定值,并求出這個定值.
為定值,并求出這個定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】正三棱柱ABC﹣A1B1C1底邊長為2,E,F分別為BB1 , AB的中點. (I)已知M為線段B1A1上的點,且B1A1=4B1M,求證:EM∥面A1FC;
(II)若二面角E﹣A1C﹣F所成角的余弦值為 ![]() ,求AA1的值.
,求AA1的值.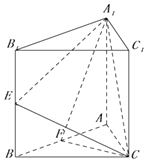
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若對于定義在![]() 上的函數
上的函數![]() ,其圖象是連續不斷的,且存在常數
,其圖象是連續不斷的,且存在常數![]() 使得
使得![]() 對任意實數
對任意實數![]() 都成立,則稱
都成立,則稱![]() 是一個“
是一個“![]() 特征函數”.下列結論中正確的個數為( )
特征函數”.下列結論中正確的個數為( )
①![]() 是常數函數中唯一的“
是常數函數中唯一的“![]() 特征函數”;
特征函數”;
②![]() 不是“
不是“![]() 特征函數”;
特征函數”;
③“![]() 特征函數”至少有一個零點;
特征函數”至少有一個零點;
④![]() 是一個“
是一個“![]() 特征函數”.
特征函數”.
A.1B.2C.3D.4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱柱ABCD﹣A1B1C1D1中,側面ADD1A1和側面CDD1C1都是矩形,BC∥AD,△ABD是邊長為2的正三角形,E,F分別為AD,A1D1的中點. 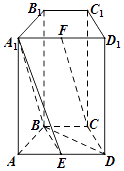
(Ⅰ)求證:DD1⊥平面ABCD;
(Ⅱ)求證:平面A1BE⊥平面ADD1A1;
(Ⅲ)若CF∥平面A1BE,求棱BC的長度.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知幾何體ABCDEF中,AB∥CD,AD⊥DC,EA⊥平面ABCD,FC∥EA,AB=AD=EA=1,CD=CF=2. 
(Ⅰ)求證:平面EBD⊥平面BCF;
(Ⅱ)求點B到平面ECD的距離.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com