
【題目】已知函數![]() 在區間
在區間![]() 上的最大值為4,最小值為1.
上的最大值為4,最小值為1.
(1)求實數![]() 、
、![]() 的值;
的值;
(2)記![]() ,若
,若![]() 在
在![]() 上是單調函數,求實數
上是單調函數,求實數![]() 的取值范圍;
的取值范圍;
(3)對于函數![]() ,用
,用![]() ,1,2,
,1,2,![]() ,
,![]() ,
,![]() 將區間
將區間![]() 任意劃分成
任意劃分成![]() 個小區間,若存在常數
個小區間,若存在常數![]() ,使得和式
,使得和式![]() 對任意的劃分恒成立,則稱函數
對任意的劃分恒成立,則稱函數![]() 為
為![]() 上的有界變差函數.記
上的有界變差函數.記![]() ,試判斷函數
,試判斷函數![]() 是否為在
是否為在![]() 上的有界變差函數?若是,求
上的有界變差函數?若是,求![]() 的最小值;若不是,請說明理由.
的最小值;若不是,請說明理由.
(參考公式:![]()
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() 或
或![]() ;(3)是,6.
;(3)是,6.
【解析】
(1)由已知中![]() 在區間
在區間![]() 的最大值為4,最小值為1,結合函數的單調性及最值,構造出關于
的最大值為4,最小值為1,結合函數的單調性及最值,構造出關于![]() ,
,![]() 的方程組,解得
的方程組,解得![]() ,
,![]() 的值;
的值;
(2)由![]() 的解析式可得
的解析式可得![]() 的解析式,討論
的解析式,討論![]() 的符號結合對勾函數的圖象和單調性可得
的符號結合對勾函數的圖象和單調性可得![]() 的范圍;
的范圍;
(3)根據有界變差函數的定義,我們先將區間![]() 進行劃分,進而判斷
進行劃分,進而判斷![]() 是否恒成立,進而得到結論.
是否恒成立,進而得到結論.
(1)![]() 函數
函數![]() ,因為
,因為![]() ,
,
所以![]() 在區間
在區間![]() 上是增函數,
上是增函數,
又![]() 函數
函數![]() 故在區間
故在區間![]() ,
,![]() 上的最大值為4,最小值為1,
上的最大值為4,最小值為1,
![]() ,即
,即![]() ,
,
解得![]() ,
,![]() ;
;
(2)由已知可得![]() ,
,
![]() ,
,
若![]() 在
在![]() 上是單調函數,
上是單調函數,
若![]() ,即
,即![]() ,由兩個增函數的和還是增函數,易得函數
,由兩個增函數的和還是增函數,易得函數![]() 在
在![]() 遞增;
遞增;
若![]() ,函數
,函數![]() 為對勾函數,結合圖象可知:在
為對勾函數,結合圖象可知:在![]() 遞增;
遞增;
![]() 或
或![]() ,解得:
,解得:![]() 或
或![]() .
.
綜上所述:![]() 或
或![]() .
.
(3)函數![]() 為
為![]() 上的有界變差函數.
上的有界變差函數.
因為函數![]() 為
為![]() 遞增,
遞增,![]() 遞減,
遞減,![]() 上的單調遞增函數,
上的單調遞增函數,
且對任意劃分![]() ,
,
有![]()
![]()
![]()
![]() 恒成立,①
恒成立,①
且對任意劃分![]() ,
,
有![]() ,
,
![]()
![]()
![]() 恒成立,②
恒成立,②
且對任意劃分![]() ,
,
有![]()
![]() ,
,
![]()
![]()
![]() 恒成立,③
恒成立,③
![]() 由①②③可得
由①②③可得![]() ,
,
![]() 存在常數
存在常數![]() ,使得
,使得![]() 恒成立,
恒成立,![]() 的最小值為6.
的最小值為6.


 小學課時特訓系列答案
小學課時特訓系列答案科目:高中數學 來源: 題型:
【題目】某超市隨機選取1000位顧客,記錄了他們購買甲、乙、丙、丁四種商品的情況,整理成如下統計表,其中“√”表示購買,“×”表示未購買.
(I)估計顧客同時購買乙和丙的概率;
(II)估計顧客在甲、乙、丙、丁中同時購買3中商品的概率;
(III)如果顧客購買了甲,則該顧客同時購買乙、丙、丁中那種商品的可能性最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(2015·陜西)在直角坐標系xOy中,直線l的參數方程為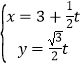 (t為參數).以原點為極點,x軸正半軸為極軸建立極坐標系,
(t為參數).以原點為極點,x軸正半軸為極軸建立極坐標系,![]() c的極坐標方程為
c的極坐標方程為![]() =2
=2![]() sin
sin![]() .
.
(1)寫出![]() c的直角坐標方程;
c的直角坐標方程;
(2)P為直線l上一動點,當P到圓心C的距離最小時,求P的直角坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若將函數y=2sin 2x的圖像向左平移 ![]() 個單位長度,則評議后圖象的對稱軸為( )
個單位長度,則評議后圖象的對稱軸為( )
A.x= ![]() –
– ![]() (k∈Z)
(k∈Z)
B.x= ![]() +
+ ![]() (k∈Z)
(k∈Z)
C.x= ![]() –
– ![]() (k∈Z)
(k∈Z)
D.x= ![]() +
+ ![]() (k∈Z)
(k∈Z)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(選修4﹣1:幾何證明選講)
如圖,直線AB為圓的切線,切點為B,點C在圓上,∠ABC的角平分線BE交圓于點E,DB垂直BE交圓于D.
(1)證明:DB=DC;
(2)設圓的半徑為1,BC= ![]() ,延長CE交AB于點F,求△BCF外接圓的半徑.
,延長CE交AB于點F,求△BCF外接圓的半徑.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已成橢圓 ![]() 的左右頂點分別為
的左右頂點分別為 ![]() ,上下頂點分別為
,上下頂點分別為 ![]() ,左右焦點分別為
,左右焦點分別為 ![]() ,其中長軸長為4,且圓
,其中長軸長為4,且圓 ![]() 為菱形
為菱形 ![]() 的內切圓.
的內切圓.
(1)求橢圓 ![]() 的方程;
的方程;
(2)點 ![]() 為
為 ![]() 軸正半軸上一點,過點
軸正半軸上一點,過點 ![]() 作橢圓
作橢圓 ![]() 的切線
的切線 ![]() ,記右焦點
,記右焦點 ![]() 在
在 ![]() 上的射影為
上的射影為 ![]() ,若
,若 ![]() 的面積不小于
的面積不小于 ![]() ,求
,求 ![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若函數f(x)在其圖像上存在不同的兩點A(x1 , y1),B(x2 , y2),其坐標滿足條件:|x1x2+y1y2|﹣ ![]() 的最大值為0,則稱f(x)為“柯西函數”, 則下列函數:
的最大值為0,則稱f(x)為“柯西函數”, 則下列函數:
①f(x)=x+ ![]() (x>0);
(x>0);
②f(x)=lnx(0<x<3);
③f(x)=2sinx;
④f(x)= ![]() .
.
其中為“柯西函數”的個數為( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐P﹣ABCD中,△PAD為正三角形,AB∥CD,AB=2CD,∠BAD=90°,PA⊥CD,E為棱PB的中點 (Ⅰ)求證:平面PAB⊥平面CDE;
(Ⅱ)若直線PC與平面PAD所成角為45°,求二面角A﹣DE﹣C的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com