【題目】某車間計劃每天生產卡車模型、賽車模型、小汽車模型這三種玩具共100個，已知生產一個卡車模型需5分鐘，生產一個賽車模型需7分鐘，生產一個小汽車模型需4分鐘，且生產一個卡車模型可獲利潤8元，生產一個賽車模型可獲利潤9元，生產一個小汽車模型可獲利潤6元．若總生產時間不超過10小時，該公司合理分配生產任務使每天的利潤最大，則最大利潤是______________元．
名校課堂系列答案科目：高中數學 來源： 題型：
【題目】某校從高一年級學生中隨機抽取40名中學生，將他們的期中考試數學成績（滿分100分，成績均為不低于40分的整數）分成六段： 
， 
，…， 
，得到如圖所示的頻率分布直方圖.
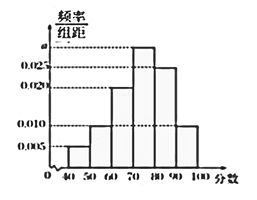
（1）求圖中實數
的值；
（2）若該校高一年級共有640人，試估計該校高一年級期中考試數學成績不低于60分的人數；
（3）若從數學成績在
與
兩個分數段內的學生中隨機選取2名學生，求這2名學生的數學成績之差的絕對值不大于10的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某市春節期間7家超市的廣告費支出
（萬元）和銷售額
（萬元）數據如下：
超市 | A | B | C | D | E | F | G |
廣告費支出 | 1 | 2 | 4 | 6 | 11 | 13 | 19 |
銷售額 | 19 | 32 | 40 | 44 | 52 | 53 | 54 |
（1）若用線性回歸模型擬合
與
的關系，求關于的線性回歸方程；
（2）用二次函數回歸模型擬合與的關系，可得回歸方程：
，
經計算二次函數回歸模型和線性回歸模型的
分別約為
和
，請用說明選擇哪個回歸模型更合適，并用此模型預測
超市廣告費支出為3萬元時的銷售額．
參數數據及公式：
，
，
．
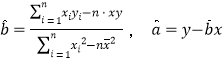查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知圓
： 
和點
，動圓
經過點
且與圓
相切，圓心
的軌跡為曲線
．
（1）求曲線
的方程；
（2）點
是曲線
與
軸正半軸的交點，點
， 
在曲線
上，若直線
， 
的斜率分別是
， 
，滿足
，求
面積的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】選修4-4：坐標系與參數方程
在直角坐標系
中，直線
的方程為
，曲線
的參數方程為
（
為參數）．
（1）已知在極坐標系（與直角坐標系
取相同的長度單位，且以原點
為極點，以
軸正半軸為極軸）中，點
的極坐標為
，判斷點
與曲線
的位置關系；
（2）設點
是曲線
上的一個動點，求它到直線
的距離的最小值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=
的定義域為A，集合B={x|（x﹣m﹣3）（x﹣m+3）≤0}．
（1）求A和f（x）的值域C；
（2）若A∩B=[2，3]，求實數m的值；
（3）若CRB，求實數m的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】全世界人們越來越關注環境保護問題，某監測站點于2016年8月某日起連續
天監測空氣質量指數（
），數據統計如下：
（1）根據所給統計表和頻率分布直方圖中的信息求出
的值，并完成頻率分布直方圖；
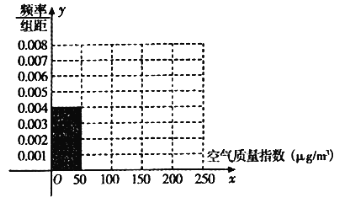
（2）由頻率分布直方圖求該組數據的平均數與中位數；
（3）在空氣質量指數分別屬于
和
的監測數據中，用分層抽樣的方法抽取5天，再從中任意選取2天，求事件
“兩天空氣都為良”發生的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知定義域為R的函數f（x）=
是奇函數．
（1）求a，b的值；
（2）判斷函數f（x）的單調性，并用定義證明；
（3）若對于任意
都有f（kx2）+f（2x﹣1）＞0成立，求實數k的取值范圍．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
