【題目】某市環保部門對該市市民進行了一次垃圾分類知識的網絡問卷調查，每一位市民僅有一次參加機會，通過隨機抽樣，得到參加問卷調查的
人的得分（滿分：
分）數據，統計結果如下表所示．
組別 |
|
|
|
|
|
|
|
頻數 |
|
|
|
|
|
|
|
（1）已知此次問卷調查的得分
服從正態分布
，
近似為這人得分的平均值（同一組中的數據用該組區間的中點值為代表），請利用正態分布的知識求
；
（2）在（1）的條件下，環保部門為此次參加問卷調查的市民制定如下獎勵方案.
（ⅰ）得分不低于的可以獲贈
次隨機話費，得分低于的可以獲贈
次隨機話費；
（ⅱ）每次贈送的隨機話費和相應的概率如下表.
贈送的隨機話費/元 |
|
|
概率 |
|
|
現市民甲要參加此次問卷調查，記
為該市民參加問卷調查獲贈的話費，求的分布列及數學期望．
附：
，若
，則
，
，
.
閱讀快車系列答案科目：高中數學 來源： 題型：
【題目】已知各項是正數的數列
的前n項和為
．
（1）若
（nN*，n≥2），且
．
①求數列的通項公式；
②若
對任意
恒成立，求實數
的取值范圍；
（2）數列是公比為q（q＞0， q1）的等比數列，且{an}的前n項積為
．若存在正整數k，對任意nN*，使得
為定值，求首項
的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某大學的
名同學準備拼車去旅游，其中大一、大二、大三、大四每個年級各兩名，分乘甲、乙兩輛汽車.每車限坐
名同學(乘同一輛車的名同學不考慮位置)，其中大一的孿生姐妹需乘同一輛車，則乘坐甲車的名同學中恰有
名同學是來自于同一年級的乘坐方式共有_______種（有數字作答）.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知拋物線C：y2=2px過點P（1，1）.過點（0， 
）作直線l與拋物線C交于不同的兩點M，N，過點M作x軸的垂線分別與直線OP，ON交于點A，B，其中O為原點.
（Ⅰ）求拋物線C的方程，并求其焦點坐標和準線方程；
（Ⅱ）求證：A為線段BM的中點.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知圓C過點A(2,6),且與直線l1: x+y－10=0相切于點B(6,4).
(1)求圓C的方程；
(2)過點P(6,24)的直線l2與圓C交于M,N兩點,若△CMN為直角三角形,求直線l2的斜率；
(3)在直線l3: y=x－2上是否存在一點Q,過點Q向圓C引兩切線,切點為E,F, 使△QEF為正三角形,若存在,求出點Q的坐標,若不存在,說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在三棱柱
中， 
底面
， 
， 
， 
， 
是棱
上一點．
（I）求證： 
．
（II）若
， 
分別是
， 
的中點，求證： 
平面
．
（III）若二面角
的大小為
，求線段
的長．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
，現有一組數據，將其繪制所得的莖葉圖如圖所示（其中莖為整數部分，葉為小數部分.例如：
可記為
，且上述數據的平均數為
.）
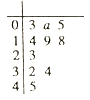
（Ⅰ）求莖葉圖中數據
的值；
（Ⅱ）現從莖葉圖中小于
的數據中任取兩個數據分別替換
的值，求恰有一個數據使得函數沒有零點的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某印刷廠為了研究單冊書籍的成本
（單位：元）與印刷冊數
（單位：千冊）之間的關系，在印制某種書籍時進行了統計，相關數據見下表：
印刷冊數 |
|
|
|
|
|
單冊成本 |
|
|
|
|
|
根據以上數據，技術人員分別借助甲、乙兩種不同的回歸模型，得到兩個回歸方程，方程甲：
，方程乙：
.
（1）為了評價兩種模型的擬合效果，完成以下任務.
①完成下表（計算結果精確到
）；
印刷冊數 |
|
|
|
|
| |
單冊成本 |
|
|
|
|
| |
模型甲 | 估計值 |
|
|
| ||
殘差 |
|
|
| |||
模型乙 | 估計值 |
|
|
| ||
殘差 |
|
|
| |||
②分別計算模型甲與模型乙的殘差平方和，并通過比較，判斷哪個模型擬合效果更好.
（2）該書上市之后，受到廣大讀者熱烈歡迎，不久便全部售罄，于是印刷廠決定進行二次印刷，根據市場調查，新需求量為
千冊，若印刷廠以每冊
元的價格將書籍出售給訂貨商，求印刷廠二次印刷千冊獲得的利潤？（按（1）中擬合效果較好的模型計算印刷單冊書的成本）.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
