
【題目】如圖,在四棱錐![]() 中,
中,![]() 底面
底面![]() ,底面
,底面![]() 為平行四邊形,
為平行四邊形,![]() ,且
,且![]() ,
,![]() ,
,![]() 是棱
是棱![]() 的中點.
的中點.
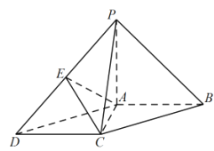
(1)求證:![]() 平面
平面![]() ;
;
(2)求直線![]() 與平面
與平面![]() 所成角的正弦值;
所成角的正弦值;
(3)在線段![]() 上(不含端點)是否存在一點
上(不含端點)是否存在一點![]() ,使得二面角
,使得二面角![]() 的余弦值為
的余弦值為![]() ?若存在,確定
?若存在,確定![]() 的位置;若不存在,請說明理由.
的位置;若不存在,請說明理由.
【答案】(1)證明見解析.(2)![]() .(3)存在,
.(3)存在,![]()
【解析】
(1)連接![]() 交
交![]() 于點
于點![]() ,連接
,連接![]() ,可證
,可證![]() ,從而得線面平行;
,從而得線面平行;
(2)由題意以![]() 為坐標原點,分別以
為坐標原點,分別以![]()
![]() 所在直線為
所在直線為![]() 軸,
軸,![]() 軸,
軸,![]() 軸建立空間直角坐標系,可用向量法求出線面角;
軸建立空間直角坐標系,可用向量法求出線面角;
(3)在(2)基礎上,設![]() ,求出平面
,求出平面![]() 和平面
和平面![]() ((2)中已有)法向量,由法向量夾角與二面角的關系可求得
((2)中已有)法向量,由法向量夾角與二面角的關系可求得![]() .
.
(1)連接![]() 交
交![]() 于點
于點![]() ,連接
,連接![]() .
.
∵![]() 是平行四邊形,∴
是平行四邊形,∴![]() 是
是![]() 的中點.又
的中點.又![]() 是
是![]() 的中點,∴
的中點,∴![]()
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ;
;
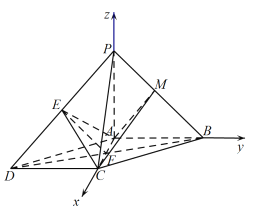
(2)以![]() 為坐標原點,分別以
為坐標原點,分別以![]()
![]() 所在直線為
所在直線為![]() 軸,
軸,![]() 軸,
軸,![]() 軸建立如圖所示的空間直角坐標系,則
軸建立如圖所示的空間直角坐標系,則![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
設平面![]() 的法向量為
的法向量為![]() .
.
∵![]() ,
,
∴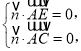 即
即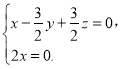
不妨取![]() ,得
,得![]()
又![]() .
.
設直線![]() 與平面
與平面![]() 所成的角為
所成的角為![]() ,
,
則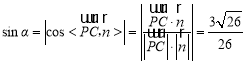 ,
,
即直線![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() .
.
(3)假設在線段![]() 上(不含端點)存在一點
上(不含端點)存在一點![]() ,使得二面角
,使得二面角![]() 的余弦值為
的余弦值為![]() .連接
.連接![]() .設
.設![]() , 得
, 得![]() .
.
設平面![]() 的法向量為
的法向量為![]() .
.
∵![]() ,
,
∴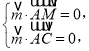 即
即![]()
不妨取![]() ,得
,得![]()
設二面角![]() 的平面角為
的平面角為![]() ,
,
則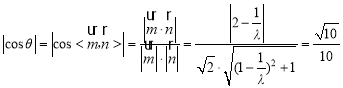 .
.
化簡得![]() ,
,
解得![]() ,或
,或![]() .
.
∵二面角![]() 的余弦值為
的余弦值為![]() ,
,
∴![]() .
.
∴在線段![]() 上存在一點
上存在一點![]() ,且
,且![]() ,使得二面角
,使得二面角![]() 的余弦值為
的余弦值為![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】近年來,隨著全球石油資源緊張、大氣污染日益嚴重和電池技術的提高,電動汽車已被世界公認為21世紀汽車工業改造和發展的主要方向.為了降低對大氣的污染和能源的消耗,某品牌汽車制造商研發了兩款電動汽車車型![]() 和車型
和車型![]() ,并在黃金周期間同時投放市場.為了了解這兩款車型在黃金周的銷售情況,制造商隨機調查了5家汽車
,并在黃金周期間同時投放市場.為了了解這兩款車型在黃金周的銷售情況,制造商隨機調查了5家汽車![]() 店的銷量(單位:臺),得到下表:
店的銷量(單位:臺),得到下表:
| 甲 | 乙 | 丙 | 丁 | 戊 |
車型 | 6 | 6 | 13 | 8 | 11 |
車型 | 12 | 9 | 13 | 6 | 4 |
(1)若從甲、乙兩家![]() 店銷售出的電動汽車中分別各自隨機抽取1臺電動汽車作滿意度調查,求抽取的2臺電動汽車中至少有1臺是車型
店銷售出的電動汽車中分別各自隨機抽取1臺電動汽車作滿意度調查,求抽取的2臺電動汽車中至少有1臺是車型![]() 的概率;
的概率;
(2)現從這5家汽車![]() 店中任選3家舉行促銷活動,用
店中任選3家舉行促銷活動,用![]() 表示其中車型
表示其中車型![]() 銷量超過車型
銷量超過車型![]() 銷量的
銷量的![]() 店的個數,求隨機變量
店的個數,求隨機變量![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知平面直角坐標系![]() 中,曲線
中,曲線![]() 的方程為
的方程為![]() ,以原點
,以原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系,直線
軸的正半軸為極軸建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]() .若將曲線
.若將曲線![]() 上的所有點的橫坐標縮小到原來的一半,縱坐標伸長到原來的
上的所有點的橫坐標縮小到原來的一半,縱坐標伸長到原來的![]() 倍,得曲線
倍,得曲線![]() .
.
(1)寫出直線![]() 和曲線
和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)設點![]() , 直線
, 直線![]() 與曲線
與曲線![]() 的兩個交點分別為
的兩個交點分別為![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某植物學家培養出一種觀賞性植物,會開出紅花或黃花,已知該植物第一代開紅花和黃花的概率都是![]() ,從第二代開始,若上一代開紅花,則這一代開紅花的概率是
,從第二代開始,若上一代開紅花,則這一代開紅花的概率是![]() ,開黃花的概率是
,開黃花的概率是![]() ;若上一代開黃花,則這一代開紅花的概率是
;若上一代開黃花,則這一代開紅花的概率是![]() ,開黃花的概率是
,開黃花的概率是![]() .記第n代開紅花的概率為
.記第n代開紅花的概率為![]() ,第n代開黃花的概率為
,第n代開黃花的概率為![]() .
.
(1)求![]() ;
;
(2)①證明:數列![]() 為等比數列;
為等比數列;
②第![]() 代開哪種顏色花的概率更大?
代開哪種顏色花的概率更大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,圓錐的底面![]() 半徑為2,
半徑為2,![]() 是圓周上的定點,動點
是圓周上的定點,動點![]() 在圓周上逆時針旋轉,設
在圓周上逆時針旋轉,設![]() (
(![]() ),
),![]() 是母線
是母線![]() 的中點,已知當
的中點,已知當![]() 時,
時,![]() 與底面所成角為
與底面所成角為![]() .
.
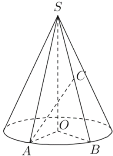
(1)求該圓錐的側面積;
(2)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示的五面體中,![]() 是正方形,
是正方形,![]() 是等腰梯形,且平面
是等腰梯形,且平面![]() 平面
平面![]() ,
,![]() 為
為![]() 的中點,
的中點,![]() ,
,![]() .
.

(1)求證:平面![]() 平面
平面![]() ;
;
(2)![]() 為線段
為線段![]() 的中點,
的中點,![]() 在線段
在線段![]() 上,記
上,記![]() ,
,![]() 是線段
是線段![]() 上的動點. 當
上的動點. 當![]() 為何值時,三棱錐
為何值時,三棱錐![]() 的體積為定值?證明此時二面角
的體積為定值?證明此時二面角![]() 為定值,并求出其余弦值.
為定值,并求出其余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市場研究人員為了了解產業園引進的甲公司前期的經營狀況,對該公司2018年連續六個月的利潤進行了統計,并根據得到的數據繪制了相應的折線圖,如圖所示
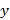
(1)由折線圖可以看出,可用線性回歸模型擬合月利潤![]() (單位:百萬元)與月份代碼
(單位:百萬元)與月份代碼![]() 之間的關系,求
之間的關系,求![]() 關于
關于![]() 的線性回歸方程,并預測該公司2019年3月份的利潤;
的線性回歸方程,并預測該公司2019年3月份的利潤;
(2)甲公司新研制了一款產品,需要采購一批新型材料,現有![]() ,
,![]() 兩種型號的新型材料可供選擇,按規定每種新型材料最多可使用
兩種型號的新型材料可供選擇,按規定每種新型材料最多可使用![]() 個月,但新材料的不穩定性會導致材料損壞的年限不相同,現對
個月,但新材料的不穩定性會導致材料損壞的年限不相同,現對![]() ,
,![]() 兩種型號的新型材料對應的產品各
兩種型號的新型材料對應的產品各![]() 件進行科學模擬測試,得到兩種新型材料使用壽命的頻數統計如下表:
件進行科學模擬測試,得到兩種新型材料使用壽命的頻數統計如下表:
使用壽命 材料類型 |
|
|
|
| 總計 |
|
|
|
|
|
|
|
|
|
|
|
|
如果你是甲公司的負責人,你會選擇采購哪款新型材料?
參考數據:![]() ,
,![]() .參考公式:回歸直線方程為
.參考公式:回歸直線方程為![]() ,其中
,其中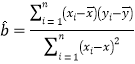
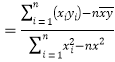 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() 是拋物線
是拋物線![]() :
:![]() 上的一點,其焦點為點
上的一點,其焦點為點![]() ,且拋物線
,且拋物線![]() 在點
在點![]() 處的切線
處的切線![]() 交圓
交圓![]() :
:![]() 于不同的兩點
于不同的兩點![]() ,
,![]() .
.
(1)若點![]() ,求
,求![]() 的值;
的值;
(2)設點![]() 為弦
為弦![]() 的中點,焦點
的中點,焦點![]() 關于圓心
關于圓心![]() 的對稱點為
的對稱點為![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com