
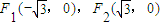 ,若曲線C內存在動點P,使得|PF1|、|OP|、|PF2|成等比數列(O為坐標原點),求
,若曲線C內存在動點P,使得|PF1|、|OP|、|PF2|成等比數列(O為坐標原點),求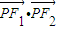 的取值范圍.
的取值范圍.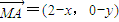 ∥(2cosθ-2,sinθ),根據共線向量定理可得⇒(x-2)sinθ=y(2cosθ-2),同理(x+2)sinθ=y(2cosθ+2),兩式相乘,即可得到點M(x,y)的軌跡方程;
∥(2cosθ-2,sinθ),根據共線向量定理可得⇒(x-2)sinθ=y(2cosθ-2),同理(x+2)sinθ=y(2cosθ+2),兩式相乘,即可得到點M(x,y)的軌跡方程;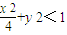 ,再由|PF1|、|OP|、|PF2|成等比數列可得
,再由|PF1|、|OP|、|PF2|成等比數列可得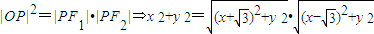
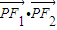 ,即可求得結果.
,即可求得結果.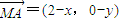 ,(2-x)sinθ+y(2cosθ-2)=0⇒(x-2)sinθ=y(2cosθ-2)①
,(2-x)sinθ+y(2cosθ-2)=0⇒(x-2)sinθ=y(2cosθ-2)①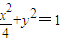 ;
;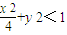 ③
③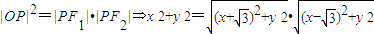
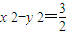 ④
④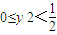
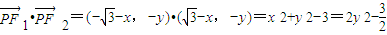
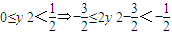


科目:高中數學 來源: 題型:
| 3 |
| 3 |
| PF1 |
| PF2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 2 |
| MN |
| ON |
查看答案和解析>>
科目:高中數學 來源:0112 月考題 題型:解答題
 ,0),F2(
,0),F2( ,0),若曲線C內存在動點P,使得|PF1|、|OP|、|PF2|成等比數列(O為坐標原點),求
,0),若曲線C內存在動點P,使得|PF1|、|OP|、|PF2|成等比數列(O為坐標原點),求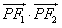 的取值范圍。
的取值范圍。 查看答案和解析>>
科目:高中數學 來源:巢湖模擬 題型:解答題
| 3 |
| 3 |
| PF1 |
| PF2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com