
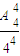 =
=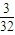 .
.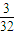 .
.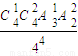 =
=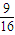 .
. .
.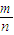 .解決此類問題,還需要考試熟練運用排列、組合的知識,并能準確求出公式中的n,m的值.
.解決此類問題,還需要考試熟練運用排列、組合的知識,并能準確求出公式中的n,m的值. 

 名題金卷系列答案
名題金卷系列答案科目:高中數學 來源:上海交通大學附屬中學2012屆度高二下學期期末考試數學 題型:填空題
把4個不同的球任意投入4個不同的盒子內(每盒裝球數不限),則無空盒的概率為________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com