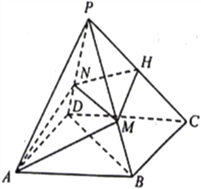
【題目】已知四棱錐
，底面
為菱形，
，
為
上的點，過
的平面分別交
，
于點
，
，且
平面
.
（1）證明：
；
（2）當為的中點，
，
與平面所成的角為
，求二面角
的余弦值.
【答案】(1)證明見解析；(2)
.
【解析】【試題分析】（1）連結
交
于點
，連結
．根據菱形有
，根據等腰三角形有
，所以以
平面
，
.利用線面平行的性質定理有
，故
，所以
.（2）以為坐標原點建立空間直角坐標系，通過計算平面
和平面
的法向量來計算二面角的余弦值.
【試題解析】
（1）證明：連結交于點，連結．因為
為菱形，所以，且為、的中點，因為
，所以
，
因為
且
平面，所以平面，
因為
平面，所以．
因為
平面
，
平面
，且平面
平面
，
所以，所以．
（2）由（1）知且，因為
，且為的中點，
所以
，所以
平面，所以
與平面所成的角為
，
所以，所以
，因為
，所以
．
分別以
，
，
為
軸，建立如圖所示空間直角坐標系，設
，則
，
所以
．
記平面的法向量為
，則
，
令
，則
，所以
，
記平面
的法向量為
，則
，
令
，則
，所以
，
記二面角
的大小為
，則
．
所以二面角的余弦值為．
名師點撥卷系列答案
英才計劃期末調研系列答案科目：高中數學 來源： 題型：
【題目】2016年10月9日，教育部考試中心下發了《關于2017年普通高考考試大綱修訂內容的通知》，在各科修訂內容中明確提出，增加中華優秀傳統文化的考核內容，積極培育和踐行社會主義核心價值觀，充分發揮高考命題的育人功能和積極導向作用.宿州市教育部門積極回應，編輯傳統文化教材，在全市范圍內開設書法課，經典誦讀等課程.為了了解市民對開設傳統文化課的態度，教育機構隨機抽取了200位市民進行了解，發現支持開展的占
，在抽取的男性市民120人中持支持態度的為80人.
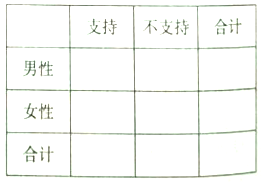
（Ⅰ）完成
列聯表，并判斷是否有
的把握認為性別與支持與否有關？
（Ⅱ）為了進一步征求對開展傳統文化的意見和建議，從抽取的200位市民中對不支持的按照分層抽樣的方法抽取5位市民，并從抽取的5人中再隨機選取2人進行座談，求選取的2人恰好為1男1女的概率.
附：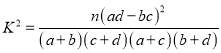 
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖是某市3月1日至14日的空氣質量指數趨勢圖．空氣質量指數小于100表示空氣質量優良，空氣質量指數大于200表示空氣重度污染．某人隨機選擇3月1日至3月13日中的某一天到達該市，并停留2天．
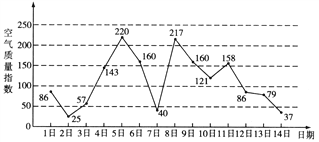
（Ⅰ）求此人到達當日空氣重度污染的概率；
（Ⅱ）設X是此人停留期間空氣質量優良的天數，求X的分布列與數學期望；
（Ⅲ）由圖判斷從哪天開始連續三天的空氣質量指數方差最大？（結論不要求證明）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在直四棱柱
中，底面
為等腰梯形，
.
（1）證明：
；
（2）設
是線段
上的動點，是否存在這樣的點，使得二面角
的余弦值為
，如果存在，求出
的長；如果不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖所示，已知A、B、C是長軸長為4的橢圓E上的三點，點A是長軸的一個端點，BC過橢圓中心O，且
，|BC|＝2|AC|．
（1）求橢圓E的方程；
（2）在橢圓E上是否存點Q，使得
？若存在，有幾個（不必求出Q點的坐標），若不存在，請說明理由．
（3）過橢圓E上異于其頂點的任一點P，作
的兩條切線，切點分別為M、N，若直線MN在x軸、y軸上的截距分別為m、n，證明：
為定值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】揚州大學數學系有6名大學生要去甲、乙兩所中學實習，每名大學生都被隨機分配到兩所中學的其中一所.
（1）求6名大學生中至少有1名被分配到甲學校實習的概率；
（2）設
，
分別表示分配到甲、乙兩所中學的大學生人數，記
，求隨機變量
的分布列和數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
