
已知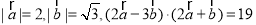 .
.
(1)求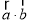 的值;(2)若
的值;(2)若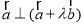 ,求
,求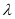 的值
的值
(1)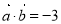 ;(2)
;(2)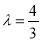 .
.
【解析】
試題分析:(1)求兩個向量的數量積有三種方法:利用定義;利用向量的坐標運算;利用數量積的幾何意義.主體應用時可根據已知條件的特征來選擇,同時要注意數量積的運算律;(2)當向量 與
與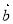 是坐標形式給出時,若證明
是坐標形式給出時,若證明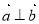 ,則只需證明
,則只需證明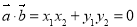 ;(3)當
;(3)當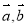 是非坐標形式時,要把
是非坐標形式時,要把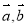 用已知的不共線的向量作為基底來表示且不共線的向量要知道其模與夾角,從而進行證明
用已知的不共線的向量作為基底來表示且不共線的向量要知道其模與夾角,從而進行證明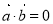 ;(4)利用向量垂直于平行的條件進行構造方程或函數是求參數或最值問題常用的方法與技巧.
;(4)利用向量垂直于平行的條件進行構造方程或函數是求參數或最值問題常用的方法與技巧.
試題解析:(1)由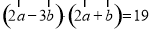 ,可得
,可得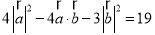 .
.
∵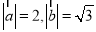 ,∴
,∴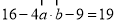 , 4分
, 4分
∴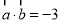 . 6分
. 6分
由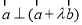 ,可得
,可得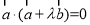 , 8分
, 8分
即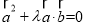 , 9分
, 9分
由(1)及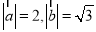 ,得
,得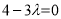 , 11分
, 11分
解得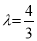 . 12分
. 12分
考點:(1)求平面向量的數量積;(2)向量垂直的應用.


科目:高中數學 來源: 題型:
|
| A、2或4或8 |
| B、4或5或8 |
| C、4或5或32 |
| D、4或5或16 |
查看答案和解析>>
科目:高中數學 來源:2016屆廣東省東莞市高一下學期教學質量檢查數學試卷(解析版) 題型:解答題
已知圓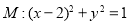 ,
,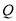 是直線
是直線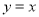 上的動點,
上的動點,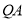 、
、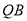 與圓
與圓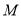 相切,切點分別為點
相切,切點分別為點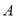 、
、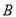 .
.
(1)若點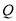 的坐標為
的坐標為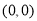 ,求切線
,求切線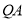 、
、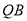 的方程;
的方程;
(2)若點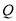 的坐標為
的坐標為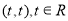 ,求直線
,求直線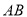 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源:2016屆內蒙古高一下學期期末考試數學試卷(解析版) 題型:選擇題
已知函數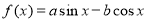 (
(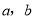 為常數,
為常數,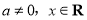 )的圖象關于
)的圖象關于
直線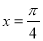 對稱,則函數
對稱,則函數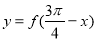 是( )
是( )
A.偶函數且它的圖象關于點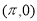 對稱
對稱
B.偶函數且它的圖象關于點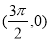 對稱
對稱
C.奇函數且它的圖象關于點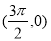 對稱
對稱
D.奇函數且它的圖象關于點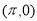 對稱
對稱
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com