
【題目】求具有下述性質的所有正整數![]() :對任意正整數
:對任意正整數![]() ,
,![]() .
.
【答案】所求的![]() 為
為![]() .
.
【解析】
對正整數![]() ,設
,設![]() 為正整數
為正整數![]() 的標準分解中素因子2的方冪.則
的標準分解中素因子2的方冪.則![]() ,
,
其中![]() 表示正整數
表示正整數![]() 在二進制表示下的數碼之和,原命題等價于求所有正整數
在二進制表示下的數碼之和,原命題等價于求所有正整數![]() ,使得對任意正整數
,使得對任意正整數![]() ,有
,有![]() .再證明所有符號條件的
.再證明所有符號條件的![]() 為
為![]() .
.
對正整數![]() ,設
,設![]() 為正整數
為正整數![]() 的標準分解中素因子2的方冪.則
的標準分解中素因子2的方冪.則
![]() , ①
, ①
其中,![]() 表示正整數
表示正整數![]() 在二進制表示下的數碼之和.
在二進制表示下的數碼之和.
由![]()
![]() .
.
進而,由式①知本題等價于求所有正整數![]() ,使得對任意正整數
,使得對任意正整數![]() ,有
,有![]() .
.
接下來證明:所有符號條件的![]() 為
為.
一方面,因為對任意正整數![]() ,有
,有![]() ,所以,
,所以,![]() 符合條件.
符合條件.
另一方面,若![]() 不為2的方冪,設
不為2的方冪,設![]() (
(![]() ,
,![]() 為大于1的奇數).
為大于1的奇數).
下面構造一個正整數![]() ,使得
,使得![]() .
.
因為![]() ,所以,問題等價于選取
,所以,問題等價于選取![]() 的一個倍數
的一個倍數![]() ,使得
,使得![]() .
.
由![]() ,知存在正整數
,知存在正整數![]() ,使得
,使得![]() .
.
事實上,由歐拉定理,知![]() 可以取
可以取![]() .
.
設奇數![]() 的二進制表示為
的二進制表示為![]() ,其中,
,其中,![]() ,
,![]() .
.
取![]() .
.
則![]() ,且
,且![]() .
.
故![]()
![]()
![]() . ②
. ②
由于![]() ,故正整數
,故正整數![]() 的二進制表示中的最高次冪小于
的二進制表示中的最高次冪小于![]() .
.
由此,對任意整數![]() 、
、![]() ,數
,數![]() 與
與![]() 的二進制表示中沒有相同的項.
的二進制表示中沒有相同的項.
又![]() ,則
,則![]() 的二進制表示中均不包含1.
的二進制表示中均不包含1.
故由式②知
![]() .
.
因此,上述選取的![]() 滿足要求.
滿足要求.
綜上,所求的![]() 為
為![]() .
.


 寶貝計劃期末沖刺奪100分系列答案
寶貝計劃期末沖刺奪100分系列答案 能考試全能100分系列答案
能考試全能100分系列答案科目:高中數學 來源: 題型:
【題目】已知點![]() 在雙曲線
在雙曲線![]()
![]() (
(![]() ,
,![]() )上,且雙曲線的一條漸近線的方程是
)上,且雙曲線的一條漸近線的方程是![]() .
.
(1)求雙曲線![]() 的方程;
的方程;
(2)若過點![]() 且斜率為
且斜率為![]() 的直線
的直線![]() 與雙曲線
與雙曲線![]() 有兩個不同的交點,求實數
有兩個不同的交點,求實數![]() 的取值范圍;
的取值范圍;
(3)設(2)中直線![]() 與雙曲線
與雙曲線![]() 交于
交于![]() 兩個不同的點,若以線段
兩個不同的點,若以線段![]() 為直徑的圓經過坐標原點,求實數
為直徑的圓經過坐標原點,求實數![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (
(![]() 為常數,
為常數,![]() 且
且![]() ),且數列
),且數列![]() 是首項為
是首項為![]() ,公差為
,公差為![]() 的等差數列.
的等差數列.
(1)求證:數列![]() 是等比數列;
是等比數列;
(2)若![]() ,當
,當![]() 時,求數列
時,求數列![]() 的前
的前![]() 項和
項和![]() 的最小值;
的最小值;
(3)若![]() ,問是否存在實數
,問是否存在實數![]() ,使得
,使得![]() 是遞增數列?若存在,求出
是遞增數列?若存在,求出![]() 的范圍;若不存在,說明理由.
的范圍;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校興趣小組在如圖所示的矩形區域![]() 內舉行機器人攔截挑戰賽,在
內舉行機器人攔截挑戰賽,在![]() 處按
處按![]() 方向釋放機器人甲,同時在
方向釋放機器人甲,同時在![]() 處按某方向釋放機器人乙,設機器人乙在
處按某方向釋放機器人乙,設機器人乙在![]() 處成功攔截機器人甲,若點
處成功攔截機器人甲,若點![]() 在矩形區城
在矩形區城![]() 內(包含邊界),則挑戰成功,否則挑戰失敗,已知
內(包含邊界),則挑戰成功,否則挑戰失敗,已知![]() 米,
米,![]() 為
為![]() 中點,機器人乙的速度是機器人甲的速度的2倍,比賽中兩機器人均按勻速直線遠動方式行進.
中點,機器人乙的速度是機器人甲的速度的2倍,比賽中兩機器人均按勻速直線遠動方式行進.
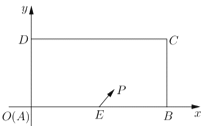
(1)如圖建系,求![]() 的軌跡方程;
的軌跡方程;
(2)記![]() 與
與![]() 的夾角為
的夾角為![]() ,
,![]() ,如何設計
,如何設計![]() 的長度,才能確保無論
的長度,才能確保無論![]() 的值為多少,總可以通過設置機器人乙的釋放角度使之挑戰成功?
的值為多少,總可以通過設置機器人乙的釋放角度使之挑戰成功?
(3)若![]() 與
與![]() 的夾角為
的夾角為![]() ,
,![]() 足夠長,則如何設置機器人乙的釋放角度,才能挑戰成功?
足夠長,則如何設置機器人乙的釋放角度,才能挑戰成功?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐P﹣ABCD中,底面ABCD是一個菱形,三角形PAD是一個等腰三角形,∠BAD=∠PAD=![]() ,點E在線段PC上,且PE=3EC.
,點E在線段PC上,且PE=3EC.
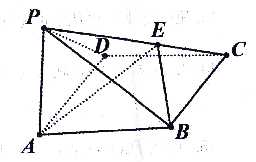
(1)求證:AD⊥PB;
(2)若平面PAD⊥平面ABCD,求二面角E﹣AB﹣P的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com