
【題目】請從下面三個條件中任選一個,補充在下面的橫線上,并作答.
①AB⊥BC,②FC與平面ABCD所成的角為![]() ,③∠ABC
,③∠ABC![]() .
.
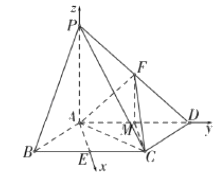
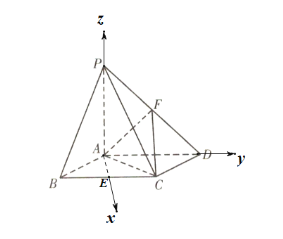
如圖,在四棱錐P﹣ABCD中,底面ABCD是菱形,PA⊥平面ABCD,且PA=AB=2,,PD的中點為F.
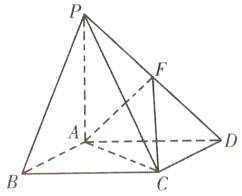
(1)在線段AB上是否存在一點G,使得AF![]() 平面PCG?若存在,指出G在AB上的位置并給以證明;若不存在,請說明理由;
平面PCG?若存在,指出G在AB上的位置并給以證明;若不存在,請說明理由;
(2)若_______,求二面角F﹣AC﹣D的余弦值.
【答案】(1)存在,G是線段AB的中點,證明見解析;(2)詳見解析
【解析】
(1)設PC的中點為H,連結FH,由題意得AGHF為平行四邊形,則AF∥GH,由此能證明在線段AB上存在中點G,使得AF∥平面PCG.
(2)選擇①AB⊥BC,推導出AB,AD,AP彼此兩兩垂直,以AB,AD,AP分別為x,y,z軸,建立空間直角坐標系,利用向量法能求出二面角F﹣AC﹣D的余弦值.選擇②FC與平面ABCD所成的角為![]() ,取BC中點E,連結AE,取AD的中點M,連結FM,CM,則FM∥PA,且FM=1,FM⊥平面ABCD,FC與平面ABCD所成角為∠FCM,
,取BC中點E,連結AE,取AD的中點M,連結FM,CM,則FM∥PA,且FM=1,FM⊥平面ABCD,FC與平面ABCD所成角為∠FCM,![]() ,推導出AE,AD,AP彼此兩兩垂直,以AE、AD、AP分別為x,y,z軸,建立空間直角坐標系,利用向量法能求出二面角F﹣AC﹣D的余弦值.選擇③∠ABC
,推導出AE,AD,AP彼此兩兩垂直,以AE、AD、AP分別為x,y,z軸,建立空間直角坐標系,利用向量法能求出二面角F﹣AC﹣D的余弦值.選擇③∠ABC![]() ,推導出PA⊥BC,取BC中點E,連結AE,推導出 AE,AD,AP彼此兩兩垂直,以AE、AD、AP分別為x,y,z軸,建立空間直角坐標系,利用向量法能求出二面角F﹣AC﹣D的余弦值.
,推導出PA⊥BC,取BC中點E,連結AE,推導出 AE,AD,AP彼此兩兩垂直,以AE、AD、AP分別為x,y,z軸,建立空間直角坐標系,利用向量法能求出二面角F﹣AC﹣D的余弦值.
(1)在線段AB上存在中點G,使得AF∥平面PCG.
證明如下:如圖所示:
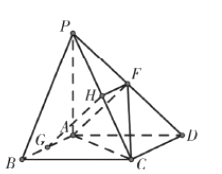
設PC的中點為H,連結FH,
因為![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]()
所以四邊形AGHF為平行四邊形,
則AF∥GH,
又GH平面PGC,AF平面PGC,
∴AF∥平面PGC.
(2)選擇①AB⊥BC:
∵PA⊥平面ABCD,∴PA⊥BC,
由題意知AB,AD,AP彼此兩兩垂直,
以AB,AD,AP分別為x,y,z軸,建立空間直角坐標系,
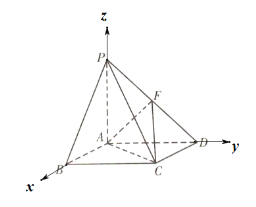
∵PA=AB=2,
則A(0,0,0),B(2,0,0),C(2,2,0),D(0,2,0),F(0,1,1),P(0,0,2),
∴![]() (0,1,1),
(0,1,1),![]() (﹣2,﹣1,1),
(﹣2,﹣1,1),
設平面FAC的一個法向量為![]() (x,y,z),
(x,y,z),
∴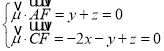 ,
,
取y=1,得![]() (﹣1,1,﹣1),
(﹣1,1,﹣1),
平面ACD的一個法向量為![]() (0,0,1),
(0,0,1),
設二面角F﹣AC﹣D的平面角為θ,
則cosθ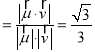 ,
,
∴二面角F﹣AC﹣D的余弦值為![]() .
.
選擇②FC與平面ABCD所成的角為![]() :
:
∵PA⊥平面ABCD,取BC中點E,連結AE,取AD的中點M,連結FM,CM,
則FM∥PA,且FM=1,
∴FM⊥平面ABCD,
FC與平面ABCD所成角為∠FCM,∴![]() ,
,
在Rt△FCM中,CM![]() ,
,
又CM=AE,∴AE2+BE2=AB2,∴BC⊥AE,
∴AE,AD,AP彼此兩兩垂直,
以AE、AD、AP分別為x,y,z軸,建立空間直角坐標系,
∵PA=AB=2,
∴A( 0,0,0),B( ![]() ,﹣1,0),C(
,﹣1,0),C(![]() ,1,0),D(0,2,0),E(
,1,0),D(0,2,0),E(![]() ,0,0),F(0,1,1),P(0,0,2),
,0,0),F(0,1,1),P(0,0,2),
∴![]() (0,1,1),
(0,1,1),![]() (
(![]() ,0,1),
,0,1),
設平面EAC的一個法向量為![]() (x,y,z),
(x,y,z),
則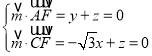 ,
,
取x![]() ,得
,得![]() (
(![]() ,﹣3,3),
,﹣3,3),
平面ACD的一個法向量為:![]() (0,0,1),
(0,0,1),
設二面角F﹣AC﹣D的平面角為θ,
則cosθ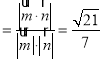 .
.
∴二面角F﹣AC﹣D的余弦值為![]() .
.
選擇③∠ABC![]() :
:
∵PA⊥平面ABCD,
∴PA⊥BC,取BC中點E,連結AE,
∵底面ABCD是菱形,∠ABC=60°,∴△ABC是正三角形,
∵E是BC的中點,∴BC⊥AE,
∴AE,AD,AP彼此兩兩垂直,
以AE、AD、AP分別為x,y,z軸,建立空間直角坐標系,
∵PA=AB=2,
∴A( 0,0,0),B( ![]() ,﹣1,0),C(
,﹣1,0),C(![]() ,1,0),D(0,2,0),E(
,1,0),D(0,2,0),E(![]() ,0,0),F(0,1,1),P(0,0,2),
,0,0),F(0,1,1),P(0,0,2),
∴![]() (0,1,1),
(0,1,1),![]() (
(![]() ,0,1),
,0,1),
設平面EAC的一個法向量為![]() (x,y,z),
(x,y,z),
則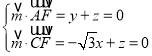 ,
,
取x![]() ,得
,得![]() (
(![]() ,﹣3,3),
,﹣3,3),
平面ACD的法向量![]() (0,0,1),
(0,0,1),
設二面角F﹣AC﹣D的平面角為θ,
θ則cosθ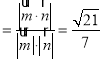 .
.
∴二面角F﹣AC﹣D的余弦值為![]() .
.


科目:高中數學 來源: 題型:
【題目】某同學計劃用他姓名的首字母![]() ,身份證的后4位數字(4位數字都不同)以及3個符號
,身份證的后4位數字(4位數字都不同)以及3個符號![]() 設置一個六位的密碼.若
設置一個六位的密碼.若![]() 必選,且符號不能超過兩個,數字不能放在首位和末位,字母和數字的相對順序不變,則他可設置的密碼的種數為( )
必選,且符號不能超過兩個,數字不能放在首位和末位,字母和數字的相對順序不變,則他可設置的密碼的種數為( )
A.864B.1009C.1225D.1441
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國是世界上嚴重缺水的歸家之一,某市為了制訂合理的節水方案,對家庭用水情況進行了抽樣調查,獲得了某年100個家庭的月均用水量(單位:![]() )的數據,將這些數據按照
)的數據,將這些數據按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成9組,制成了如圖所示的頻率分布直方圖.
分成9組,制成了如圖所示的頻率分布直方圖.
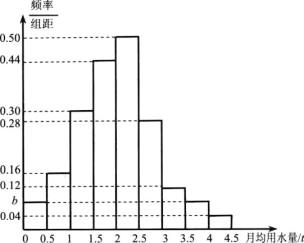
(1)求圖中的![]() 值,若該市有30萬個家庭,試估計全市月均用水量不低于
值,若該市有30萬個家庭,試估計全市月均用水量不低于![]() 的家庭數;
的家庭數;
(2)假設同組中的每個數據都用該組區間的中點值代替,試估計全市家庭月均用水量的平均數;
(3)現從月均用水量在![]() ,
,![]() 的家庭中,先按照分層抽樣的方法抽取9個家庭,再從這9家庭中抽取4個家庭,記這4個家庭中月均用水量在
的家庭中,先按照分層抽樣的方法抽取9個家庭,再從這9家庭中抽取4個家庭,記這4個家庭中月均用水量在![]() 中的數量為
中的數量為![]() ,求
,求![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國新型冠狀病毒肺炎疫情期間,以網絡購物和網上服務所代表的新興消費展現出了強大的生命力,新興消費將成為我國消費增長的新動能.某市為了了解本地居民在2020年2月至3月兩個月網絡購物消費情況,在網上隨機對1000人做了問卷調查,得如下頻數分布表:
網購消費情況(元) |
|
|
|
|
|
頻數 | 300 | 400 | 180 | 60 | 60 |
(1)作出這些數據的頻率分布直方圖,并估計本市居民此期間網絡購物的消費平均值;
(2)在調查問卷中有一項是填寫本人年齡,為研究網購金額和網購人年齡的關系,以網購金額是否超過4000元為標準進行分層抽樣,從上述1000人中抽取200人,得到如下列聯表,請將表補充完整并根據列聯表判斷,在此期間是否有95%的把握認為網購金額與網購人年齡有關.
網購不超過4000元 | 網購超過4000元 | 總計 | |
40歲以上 | 75 | 100 | |
40歲以下(含40歲) | |||
總計 | 200 |
參考公式和數據:![]() .(其中
.(其中![]() 為樣本容量)
為樣本容量)
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 則x∈[﹣1,e]時,f(x)的最小值為_____;設g(x)=[f(x)]2﹣f(x)+a若函數g(x)有6個零點,則實數a的取值范圍是_____.
則x∈[﹣1,e]時,f(x)的最小值為_____;設g(x)=[f(x)]2﹣f(x)+a若函數g(x)有6個零點,則實數a的取值范圍是_____.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() ,曲線
,曲線![]() (
(![]() 為參數),以坐標原點
為參數),以坐標原點![]() 為極點,以
為極點,以![]() 軸的正半軸為極軸建立極坐標系.
軸的正半軸為極軸建立極坐標系.
(1)求![]() 的極坐標方程;
的極坐標方程;
(2)射線![]() 的極坐標方程為
的極坐標方程為![]() ,若
,若![]() 分別與
分別與![]() 交于異于極點的
交于異于極點的![]() 兩點,求
兩點,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在極坐標系中,極點為![]() ,一條封閉的曲線
,一條封閉的曲線![]() 由四段曲線組成:
由四段曲線組成:![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)求該封閉曲線所圍成的圖形面積;
(2)若直線![]() :
:![]() 與曲線
與曲線![]() 恰有3個公共點,求
恰有3個公共點,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下圖是2020年2月15日至3月2日武漢市新增新冠肺炎確診病例的折線統計圖.則下列說法不正確的是( )
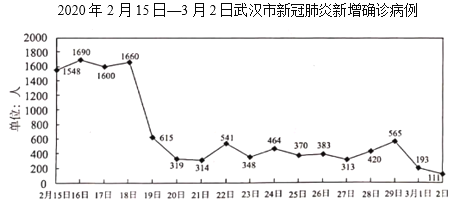
A.2020年2月19日武漢市新增新冠肺炎確診病例大幅下降至三位數
B.武漢市在新冠肺炎疫情防控中取得了階段性的成果,但防控要求不能降低
C.2020年2月19日至3月2日武漢市新增新冠肺炎確診病例低于400人的有8天
D.2020年2月15日到3月2日武漢市新增新冠肺炎確診病例最多的一天比最少的一天多1549人
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com