
【題目】某地級市共有![]() 中學生,其中有
中學生,其中有![]() 學生在
學生在![]() 年享受了“國家精準扶貧”政策,在享受“國家精準扶貧”政策的學生中困難程度分為三個等次:一般困難、很困難、特別困難,且人數之比為
年享受了“國家精準扶貧”政策,在享受“國家精準扶貧”政策的學生中困難程度分為三個等次:一般困難、很困難、特別困難,且人數之比為![]() ,為進一步幫助這些學生,當地市政府設立“專項教育基金”,對這三個等次的困難學生每年每人分別補助
,為進一步幫助這些學生,當地市政府設立“專項教育基金”,對這三個等次的困難學生每年每人分別補助![]() 元、
元、![]() 元、
元、![]() 元.經濟學家調查發現,當地人均可支配年收入較上一年每增加
元.經濟學家調查發現,當地人均可支配年收入較上一年每增加![]() ,一般困難的學生中有
,一般困難的學生中有![]() 會脫貧,脫貧后將不再享受“精準扶貧”政策,很困難的學生有
會脫貧,脫貧后將不再享受“精準扶貧”政策,很困難的學生有![]() 轉為一般困難學生,特別困難的學生中有
轉為一般困難學生,特別困難的學生中有![]() 轉為很困難學生.現統計了該地級市
轉為很困難學生.現統計了該地級市![]() 年到
年到![]() 年共
年共![]() 年的人均可支配年收入,對數據初步處理后得到了如圖所示的散點圖和表中統計量的值,其中年份
年的人均可支配年收入,對數據初步處理后得到了如圖所示的散點圖和表中統計量的值,其中年份![]() 取
取![]() 時代表
時代表![]() 年,
年,![]() 取
取![]() 時代表
時代表![]() 年,……依此類推,且
年,……依此類推,且![]() 與
與![]() (單位:萬元)近似滿足關系式
(單位:萬元)近似滿足關系式![]() .(
.(![]() 年至
年至![]() 年該市中學生人數大致保持不變)
年該市中學生人數大致保持不變)
|
|
|
|
|
|

(1)估計該市![]() 年人均可支配年收入為多少萬元?
年人均可支配年收入為多少萬元?
(2)試問該市![]() 年的“專項教育基金”的財政預算大約為多少萬元?
年的“專項教育基金”的財政預算大約為多少萬元?
附:對于一組具有線性相關關系的數據![]() ,
,![]() ,…,
,…,![]() ,其回歸直線方程
,其回歸直線方程![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為 ,
,![]() .
.
【答案】(1) ![]() ;(2)1624萬元.
;(2)1624萬元.
【解析】分析:(1)根據表中數據,求出![]() ,代入公式求值,從而得到回歸直線方程,代入
,代入公式求值,從而得到回歸直線方程,代入![]() 即可;
即可;
(2)通過由題意知![]() 年時該市享受“國家精準扶貧”政策的學生共
年時該市享受“國家精準扶貧”政策的學生共![]() 人.一般困難、很困難、特別困難的中學生依次有
人.一般困難、很困難、特別困難的中學生依次有![]() 人、
人、![]() 人、
人、![]() 人,按照增長比例關系求解2017年時該市享受“國家精準扶貧”政策的學生,即可得財政預算.
人,按照增長比例關系求解2017年時該市享受“國家精準扶貧”政策的學生,即可得財政預算.
詳解:(1)因為![]() ,所以
,所以![]() .
.
所以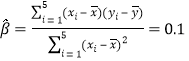 ,
,
![]() ,所以
,所以![]() .
.
當![]() 時,
時,![]() 年人均可支配年收入
年人均可支配年收入![]() (萬元).
(萬元).
(2)由題意知![]() 年時該市享受“國家精準扶貧”政策的學生共
年時該市享受“國家精準扶貧”政策的學生共![]() 人.
人.
一般困難、很困難、特別困難的中學生依次有![]() 人、
人、![]() 人、
人、![]() 人,
人,![]() 年人均可支配收入比
年人均可支配收入比![]() 年增長
年增長![]() .
.
所以![]() 年該市特別困難的中學生有
年該市特別困難的中學生有![]() 人,
人,
很困難的學生有![]() 人,
人,
一般困難的學生有![]() 人.
人.
所以![]() 年的“專項教育基金”的財政預算大約為
年的“專項教育基金”的財政預算大約為![]() (萬元).
(萬元).


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】定義在R上的函數f(x)滿足f(﹣x)=﹣f(x),f(x﹣2)=f(x+2),且x∈(﹣1,0)時,f(x)=2x+ ![]() ,則f(log220)=( )
,則f(log220)=( )
A.﹣1
B.![]()
C.1
D.﹣ ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從全校參加數學競賽的學生的試卷中抽取一個樣本,考察競賽的成績分布情況,將樣本分成5組,繪成頻率分布直方圖,圖中從左到右各小組的小長方形的高之比為1:3:6:4:2,最右邊一組頻數是6,請結合直方圖提供的信息,解答下列問題:
(1)樣本的容量是多少?
(2)列出頻率分布表;
(3)估計這次競賽中,成績高于60分的學生占總人數的百分比;
(4)成績落在哪個范圍內的人數最多?并求出該小組的頻數,頻率.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在三棱錐ABCD中,BC⊥CD,Rt△BCD斜邊上的高為1,三棱錐ABCD的外接球的直徑是AB,若該外接球的表面積為16π,則三棱錐ABCD體積的最大值為( )
A.![]()
B.![]()
C.1
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校為了解高一實驗班的數學成績,采用抽樣調查的方式,獲取了![]() 位學生在第一學期末的數學成績數據,樣本統計結果如下表:
位學生在第一學期末的數學成績數據,樣本統計結果如下表:
分組 | 頻數 | 頻率 |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
合計 |
|
|
(1)求![]() 的值和實驗班數學平均分的估計值;
的值和實驗班數學平均分的估計值;
(2)如果用分層抽樣的方法從數學成績小于![]() 分的學生中抽取
分的學生中抽取![]() 名學生,再從這
名學生,再從這![]() 名學生中選
名學生中選![]() 人,求至少有一個學生的數學成績是在
人,求至少有一個學生的數學成績是在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線![]() :
: ![]() ,
, ![]() :
: ![]() ,和兩點
,和兩點![]() (0,1),
(0,1),![]() (-1,0),給出如下結論:
(-1,0),給出如下結論:
①不論![]() 為何值時,
為何值時, ![]() 與
與![]() 都互相垂直;
都互相垂直;
②當![]() 變化時,
變化時, ![]() 與
與![]() 分別經過定點A(0,1)和B(-1,0);
分別經過定點A(0,1)和B(-1,0);
③不論![]() 為何值時,
為何值時, ![]() 與
與![]() 都關于直線
都關于直線![]() 對稱;
對稱;
④如果![]() 與
與![]() 交于點
交于點![]() ,則
,則![]() 的最大值是1;
的最大值是1;
其中,所有正確的結論的個數是( )
A. 1 B. 2 C. 3 D. 4.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)求f(2),f(x);
(2)證明:函數f(x)在[1,17]上為增函數;
(3)試求函數f(x)在[1,17]上的最大值和最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設離心率為 ![]() 的橢圓E:
的橢圓E: ![]() +
+ ![]() =1(a>b>0)的左、右焦點為F1 , F2 , 點P是E上一點,PF1⊥PF2 , △PF1F2內切圓的半徑為
=1(a>b>0)的左、右焦點為F1 , F2 , 點P是E上一點,PF1⊥PF2 , △PF1F2內切圓的半徑為 ![]() ﹣1.
﹣1.
(1)求E的方程;
(2)矩形ABCD的兩頂點C、D在直線y=x+2,A、B在橢圓E上,若矩形ABCD的周長為 ![]() ,求直線AB的方程.
,求直線AB的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的中心在坐標原點,焦點在
的中心在坐標原點,焦點在![]() 軸上,橢圓
軸上,橢圓![]() 上的點到焦點距離的最大值為3,最小值為1.
上的點到焦點距離的最大值為3,最小值為1.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)若直線![]() :
: ![]() 與橢圓
與橢圓![]() 相交于
相交于![]() ,
, ![]() 兩點(
兩點(![]() ,
, ![]() 不是左右頂點),且以
不是左右頂點),且以![]() 為直徑的圓過橢圓
為直徑的圓過橢圓![]() 的右頂點.求證:直線
的右頂點.求證:直線![]() 過定點,并求出該定點的坐標.
過定點,并求出該定點的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com