
【題目】選修4—4:坐標系與參數(shù)方程
在平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (其中
(其中![]() 為參數(shù)).以坐標原點
為參數(shù)).以坐標原點![]() 為極點,
為極點, ![]() 軸正半軸為極軸建立極坐標系并取相同的單位長度,曲線
軸正半軸為極軸建立極坐標系并取相同的單位長度,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)把曲線![]() 的方程化為普通方程,
的方程化為普通方程, ![]() 的方程化為直角坐標方程;
的方程化為直角坐標方程;
(2)若曲線![]() ,
, ![]() 相交于
相交于![]() 兩點,
兩點, ![]() 的中點為
的中點為![]() ,過點
,過點![]() 做曲線
做曲線![]() 的垂線交曲線
的垂線交曲線![]() 于
于![]() 兩點,求
兩點,求![]() .
.
【答案】(1)![]() ,
, ![]() (2)16
(2)16
【解析】試題分析:(1)先根據(jù)代入消元法將曲線![]() 的參數(shù)方程化為普通方程,利用
的參數(shù)方程化為普通方程,利用![]() 將曲線
將曲線![]() 的極坐標方程化為直角坐標方程;(2)先聯(lián)立
的極坐標方程化為直角坐標方程;(2)先聯(lián)立![]() 與
與![]() 方程,根據(jù)韋達定理以及中點坐標公式求
方程,根據(jù)韋達定理以及中點坐標公式求![]() ,設(shè)直線EF參數(shù)方程,與
,設(shè)直線EF參數(shù)方程,與![]() 方程聯(lián)立,利用韋達定理以及參數(shù)幾何意義得
方程聯(lián)立,利用韋達定理以及參數(shù)幾何意義得![]() .
.
試題解析:(1)曲線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (其中
(其中![]() 為參數(shù)),消去參數(shù)可得
為參數(shù)),消去參數(shù)可得![]() .
.
曲線![]() 的極坐標方程為
的極坐標方程為![]() ,展開為
,展開為![]() ,化為
,化為![]() ..
..
(2)設(shè)![]() ,且中點為
,且中點為![]() ,
,
聯(lián)立![]() ,
,
解得![]() ,
,
∴![]() .
.
∴![]() .
.
線段![]() 的中垂線的參數(shù)方程為
的中垂線的參數(shù)方程為
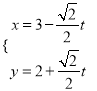 (
(![]() 為參數(shù)),
為參數(shù)),
代入![]() ,可得
,可得![]() ,
,
∴![]() ,
,
∴![]() .
.


 中考利劍中考試卷匯編系列答案
中考利劍中考試卷匯編系列答案 教育世家狀元卷系列答案
教育世家狀元卷系列答案 黃岡課堂作業(yè)本系列答案
黃岡課堂作業(yè)本系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知向量 ![]() =(sinθ,1),
=(sinθ,1), ![]() =(1,cosθ),﹣
=(1,cosθ),﹣ ![]() <θ
<θ ![]() . (Ⅰ)若
. (Ⅰ)若 ![]() ⊥
⊥ ![]() ,求tanθ的值.
,求tanθ的值.
(Ⅱ)求| ![]() +
+ ![]() |的最大值.
|的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在△ABC中,角A,B,C所對的邊長分別是a,b,c.滿足2acosC+ccosA=b.
(Ⅰ)求角C的大小;
(Ⅱ)求sinAcosB+sinB的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)  .
.
(1)請在直角坐標系中畫出函數(shù)f(x)的圖象,并寫出該函數(shù)的單調(diào)區(qū)間;
(2)若函數(shù)g(x)=f(x)﹣m恰有3個不同零點,求實數(shù)m的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】空間四邊形ABCD中,AD=BC=2,E,F(xiàn)分別是AB,CD的中點,EF= ![]() ,則異面直線AD,BC所成的角的補角為( )
,則異面直線AD,BC所成的角的補角為( ) 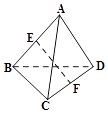
A.120°
B.60°
C.90°
D.30°
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() 其中實數(shù)
其中實數(shù)![]() 為常數(shù)且
為常數(shù)且![]() .
.
(I)求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(II)若函數(shù)![]() 既有極大值,又有極小值,求實數(shù)
既有極大值,又有極小值,求實數(shù)![]() 的取值范圍及所有極值之和;
的取值范圍及所有極值之和;
(III)在(II)的條件下,記![]() 分別為函數(shù)
分別為函數(shù)![]() 的極大值點和極小值點,
的極大值點和極小值點,
求證: ![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè){an}是各項都為正數(shù)的等比數(shù)列,{bn}是等差數(shù)列,且a1=b1=1,a3+b5=13,a5+b3=21.
(Ⅰ)求數(shù)列{an},{bn}的通項公式;
(Ⅱ)設(shè)數(shù)列{an}的前n項和為Sn , 求數(shù)列{Snbn}的前n項和Tn .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某公司租地建倉庫,每月土地占用費y1與車庫到車站的距離x成反比,而每月的庫存貨物的運費y2與車庫到車站的距離x成正比.如果在距離車站10公里處建立倉庫,這兩項費用y1和y2分別為2萬元和8萬元.求若要使得這兩項費用之和最小時,倉庫應(yīng)建在距離車站多遠處?此時最少費用為多少萬元?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
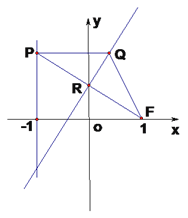
【題目】在平面直角坐標系![]() 中,設(shè)點
中,設(shè)點![]() (1,0),直線
(1,0),直線![]() :
: ![]() ,點
,點![]() 在直線
在直線![]() 上移動,
上移動, ![]() 是線段
是線段![]() 與
與![]() 軸的交點, 異于點R的點Q滿足:
軸的交點, 異于點R的點Q滿足: ![]() ,
, ![]() .
.
(1)求動點![]() 的軌跡的方程;
的軌跡的方程;
(2) 記![]() 的軌跡的方程為
的軌跡的方程為![]() ,過點
,過點![]() 作兩條互相垂直的曲線
作兩條互相垂直的曲線![]()
的弦![]() .
. ![]() ,設(shè)
,設(shè)![]() .
. ![]() 的中點分別為
的中點分別為![]() .
.
問直線![]() 是否經(jīng)過某個定點?如果是,求出該定點,
是否經(jīng)過某個定點?如果是,求出該定點,
如果不是,說明理由.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com