
(滿分20分)本題有2小題,第1小題12分,第2小題8分.
已知數列{![]() }和{
}和{![]() }滿足:對于任何
}滿足:對于任何![]() ,有
,有![]() ,
,![]() 為非零常數),且
為非零常數),且![]() .
.
(1)求數列{![]() }和{
}和{![]() }的通項公式;
}的通項公式;
(2)若![]() 是
是![]() 與
與![]() 的等差中項,試求
的等差中項,試求![]() 的值,并研究:對任意的
的值,并研究:對任意的![]() ,
,![]() 是否一定能是數列{
是否一定能是數列{![]() }中某兩項(不同于
}中某兩項(不同于![]() )的等差中項,并證明你的結論.
)的等差中項,并證明你的結論.
解:(1)【解一】由![]() 得,
得,
![]() .
.
又![]() ,
,![]() ,
,![]() .
.
所以,{![]() }是首項為1,公比為
}是首項為1,公比為![]() 的等比數列,
的等比數列,![]() .…………………………….5分
.…………………………….5分
由![]() ,得
,得
![]()
所以,當![]() 時,
時,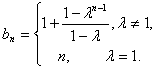 ……………………………………………….6分
……………………………………………….6分
上式對![]() 顯然成立.………………………………………………………………………..1分
顯然成立.………………………………………………………………………..1分
【解二】猜測![]() ,并用數學歸納法證明 …………………………………………….5分
,并用數學歸納法證明 …………………………………………….5分
![]() 的求法如【解一】 ………………………………………………………………………..7分
的求法如【解一】 ………………………………………………………………………..7分
【解三】猜測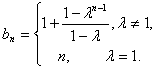 ,并用數學歸納法證明 ………………………….7分
,并用數學歸納法證明 ………………………….7分
![]() …………………………………………………………………..5分
…………………………………………………………………..5分
(2)當![]() 時,
時,![]() 不是
不是![]() 與
與![]() 的等差中項,不合題意;……………………………….1分
的等差中項,不合題意;……………………………….1分
當![]() 時,由
時,由![]()
![]() 得
得![]() ,
,
由![]() 得
得![]() (可解得
(可解得![]() )..…………………………………………2分
)..…………………………………………2分
對任意的![]() ,
,![]() 是
是![]() 與
與![]() 的等差中項. .………………………………….2分
的等差中項. .………………………………….2分
證明:![]() ,
,
![]() , .………………………………….3分
, .………………………………….3分
即,對任意的![]() ,
,![]() 是
是![]() 與
與![]() 的等差中項.
的等差中項.


科目:高中數學 來源:2011屆上海市閘北區高三第一學期期末數學理卷 題型:解答題
(滿分20分)本題有2小題,第1小題12分,第2小題8分.
已知數列{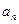 }和{
}和{ }滿足:對于任何
}滿足:對于任何 ,有
,有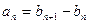 ,
, 為非零常數),且
為非零常數),且 .
.
(1)求數列{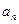 }和{
}和{ }的通項公式;
}的通項公式;
(2)若 是
是 與
與 的等差中項,試求
的等差中項,試求 的值,并研究:對任意的
的值,并研究:對任意的 ,
, 是否一定能是數列{
是否一定能是數列{ }中某兩項(不同于
}中某兩項(不同于 )的等差中項,并證明你的結論.
)的等差中項,并證明你的結論.
查看答案和解析>>
科目:高中數學 來源:2010-2011學年上海市閘北區高三第一學期期末數學理卷 題型:解答題
(滿分20分)本題有2小題,第1小題12分,第2小題8分.
已知數列{ }和{
}和{ }滿足:對于任何
}滿足:對于任何 ,有
,有 ,
, 為非零常數),且
為非零常數),且 .
.
(1)求數列{ }和{
}和{ }的通項公式;
}的通項公式;
(2)若 是
是 與
與 的等差中項,試求
的等差中項,試求 的值,并研究:對任意的
的值,并研究:對任意的 ,
, 是否一定能是數列{
是否一定能是數列{ }中某兩項(不同于
}中某兩項(不同于 )的等差中項,并證明你的結論.
)的等差中項,并證明你的結論.
查看答案和解析>>
科目:高中數學 來源:2010-2011學年上海市閘北區高三第一學期期末數學理卷 題型:解答題
(滿分20分)本題有2小題,第1小題12分,第2小題8分.
設 為定義域為
為定義域為 的函數,對任意
的函數,對任意 ,都滿足:
,都滿足: ,
, ,且當
,且當 時,
時,
(1)請指出 在區間
在區間 上的奇偶性、單調區間、最大(小)值和零點,并運用相關定義證明你關于單調區間的結論;
上的奇偶性、單調區間、最大(小)值和零點,并運用相關定義證明你關于單調區間的結論;
(2)試證明 是周期函數,并求其在區間
是周期函數,并求其在區間 上的解析式.
上的解析式.
查看答案和解析>>
科目:高中數學 來源: 題型:
(滿分20分)本題有2小題,第1小題12分,第2小題8分.
設![]() 為定義域為
為定義域為![]() 的函數,對任意
的函數,對任意![]() ,都滿足:
,都滿足:![]() ,
,![]() ,且當
,且當![]() 時,
時,![]()
(1)請指出![]() 在區間
在區間![]() 上的奇偶性、單調區間、最大(小)值和零點,并運用相關定義證明你關于單調區間的結論;
上的奇偶性、單調區間、最大(小)值和零點,并運用相關定義證明你關于單調區間的結論;
(2)試證明![]() 是周期函數,并求其在區間
是周期函數,并求其在區間![]() 上的解析式.
上的解析式.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com