
【題目】已知函數![]() ,其中e為自然對數的底數.
,其中e為自然對數的底數.
(1)若函數![]() 的圖象在點
的圖象在點![]() 處的切線方程為
處的切線方程為![]() ,求實數a的值;
,求實數a的值;
(2)若函數![]() 有2個不同的零點
有2個不同的零點![]() ,
,![]() .
.
①求實數a的取值范圍;
②求證:![]() .
.
【答案】(1)0;(2)①![]() ;②詳見解析.
;②詳見解析.
【解析】
(1)根據切線方程可知![]() ,即可求解;
,即可求解;
(2)①求函數導數,分類討論,顯然![]() 時,
時,![]() 恒成立,不符合題意,
恒成立,不符合題意,![]() 時,由導數可求函數最小值,函數有零點則最小值需小于0,得
時,由導數可求函數最小值,函數有零點則最小值需小于0,得![]() ,易知
,易知![]() 在
在![]() 上有1個零點,利用導數證明函數在
上有1個零點,利用導數證明函數在![]() 上有1個零點即可求
上有1個零點即可求![]() 的取值范圍;
的取值范圍;
②利用導數構造函數先證明當![]() ,
,![]() ,
,![]() 時,
時,![]() ,結合①可得
,結合①可得![]() ,取對數即可得出結論.
,取對數即可得出結論.
(1)因為![]() ,
,
所以切線的斜率為![]() ,解得
,解得![]() ,
,
所以實數![]() 的值為0.
的值為0.
(2)①由題意知函數![]() 的定義域為
的定義域為![]() 且
且![]() .
.
當![]() 時,
時,![]() 恒成立,
恒成立,
所以![]() 在
在![]() 上為增函數,
上為增函數,
故![]() 至多有1個零點,不合題意.
至多有1個零點,不合題意.
當![]() 時,令
時,令![]() ,則
,則![]() .
.
若![]() ,則
,則![]() ,
,
所以![]() 在
在![]() 上為增函數;
上為增函數;
若![]() ,則
,則![]() ,
,
所以![]() 在
在![]() 上為減函數.
上為減函數.
故![]() 的最小值為
的最小值為![]() .
.
依題意知![]() ,解得
,解得![]() .
.
一方面,![]() ,所以
,所以![]() 在
在![]() 上有1個零點.
上有1個零點.
另一方面,先證明![]() .
.
令![]() ,則
,則![]()
當![]() 時,
時,![]() ,故
,故![]() 在
在![]() 上為增函數;
上為增函數;
當![]() 時,
時,![]() .故
.故![]() 在
在![]() 上為減函數.
上為減函數.
所以![]() 的最大值為
的最大值為![]() ,故
,故![]() .
.
因為![]() ,所以
,所以![]() .
.
而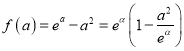 .
.
令![]() ,
,![]() ,則
,則![]()
當![]() 時,
時,![]() .故
.故![]() 在
在![]() 上為增函數,
上為增函數,
所以![]()
故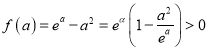
因此![]() 在
在![]() 上有1個零點,
上有1個零點,
綜上,實數![]() 的取值范圍是
的取值范圍是![]() .
.
②先證明當![]() ,
,![]() ,
,![]() 時,
時,
![]() .(*)
.(*)
不妨設![]() ,
,
(*)式等價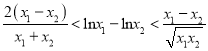 ,
,
等價于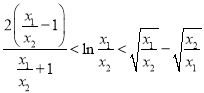
在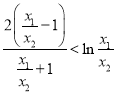 中,令
中,令![]() ,即證
,即證![]() .
.
令![]()
則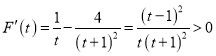 ,
,
所以![]() 在
在![]() 上為增函數,故
上為增函數,故![]() ,
,
所以![]() 成立,
成立,
所以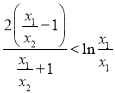 成立.
成立.
在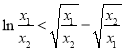 中,令
中,令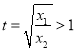 ,即證
,即證![]() .
.
令![]() ,則
,則![]() ,
,
所以![]() 在
在![]() 上為減函數,故
上為減函數,故![]() ,
,
所以![]() 成立,
成立,
所以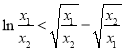 成立.
成立.
綜上,(*)式成立.
由①得![]() 有2個零點
有2個零點![]() ,
,![]() ,
,
則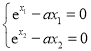 ,所以
,所以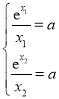 ,
,
兩邊取“![]() ”得
”得 ,
,
所以![]() .
.
利用![]() 得:
得:![]() ,
,
所以![]() 且
且![]() .
.
又因為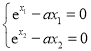
所以![]() ,
,
故![]() .
.
因此![]() .
.


科目:高中數學 來源: 題型:
【題目】設圓C滿足:①截y軸所得弦長為2;②被x軸分成兩段圓弧,其弧長的比為3:1,在滿足條件①、②的所有圓中,求圓心到直線l:x-2y=0的距離最小的圓的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某商場在促銷期間規定:商場內所有商品按標價的![]() 出售,當顧客在商場內消費一定金額后,按如下方案獲得相應金額的獎券:
出售,當顧客在商場內消費一定金額后,按如下方案獲得相應金額的獎券:
消費金額(元)的范圍 |
|
|
|
| … |
獲得獎券的金額(元) | 30 | 60 | 100 | 130 | … |
根據上述促銷方法,顧客在該商場購物可以獲得雙重優惠,例如:購買標價為400元的商品,則消費金額為320元,獲得的優惠額為:![]() 元,設購買商品得到的優惠率=(購買商品獲得的優惠額)/(商品標價),試問:
元,設購買商品得到的優惠率=(購買商品獲得的優惠額)/(商品標價),試問:
(1)若購買一件標價為1000元的商品,顧客得到的優惠率是多少?
(2)對于標價在![]() (元)內的商品,顧客購買標價為多少元的商品,可得到不小于
(元)內的商品,顧客購買標價為多少元的商品,可得到不小于![]() 的優惠率?
的優惠率?
查看答案和解析>>
科目:高中數學 來源: 題型:
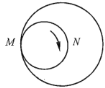
【題目】如圖,一個直徑為1的小圓沿著直徑為2的大圓內壁的逆時針方向滾動,M和N是小圓的一條固定直徑的兩個端點,那么,當小圓這樣滾過大圓內壁的一周,點M,N在大圓內所繪出的圖形大致是( )
A. B.
B. C.
C.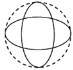 D.
D.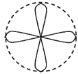
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設a>0,0≤x<2π,若函數y=cos2x-asinx+b的最大值為0,最小值為-4,試求a與b的值,并求使y取得最大值和最小值時的x值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某醫院體檢中心為回饋大眾,推出優惠活動:對首次參加體檢的人員,按200元/次收費,并注冊成為會員,對會員的后續體檢給予相應優惠,標準如下:

該休檢中心從所有會員中隨機選取了100位對他們在本中心參加體檢的次數進行統計,得到數據如表:

假設該體檢中心為顧客體檢一次的成本費用為150元,根據所給數據,解答下列問題:
(1)已知某顧客在此體檢中心參加了3次體檢,求這3次體檢,該體檢中心的平均利潤;
(2)該體檢中心要從這100人里至少體檢3次的會員中,按體檢次數用分層抽樣的方法抽出5人,再從這5人中抽取2人,每人發放現金200元.用5表示體檢3次的會員所得現金和,求![]() 的分布列及
的分布列及![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com