
在△ABC中,角A,B,C的對邊分別為a,b,c.已知2cos(B-C)+1=4cosBcosC.
(Ⅰ)求A;
(Ⅱ)若a=2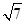 ,△ABC的面積為2
,△ABC的面積為2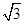 ,求b+c.
,求b+c.
(Ⅰ)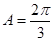 ;(Ⅱ)6.
;(Ⅱ)6.
【解析】
試題分析:(Ⅰ) 對于2cos(B-C)+1=4cosBcosC通過三角恒等變換,再結合角的范圍即可得;(Ⅱ)利用余弦定理、面積公式可求.
試題解析:(Ⅰ) 由2cos(B-C)+1=4cosBcosC,得
2(cosBcosC+sinBsinC)+1=4cosBcosC,
即2(cosBcosC-sinBsinC)=1,亦即2cos(B+C)=1,
∴cos(B+C)=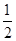 . ∵0<B+C<π,∴B+C=
. ∵0<B+C<π,∴B+C=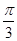 .
.
∵A+B+C=π, ∴A=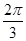 .
6分
.
6分
(Ⅱ)由(Ⅰ),得A=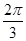 .
.
由S△ABC=2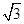 ,得
,得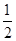 bcsin
bcsin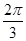 =2
=2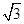 ,∴bc=8. ①
,∴bc=8. ①
由余弦定理a2=b2+c2-2bccosA,得
(2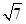 )2=b2+c2-2bccos
)2=b2+c2-2bccos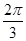 ,即b2+c2+bc=28,
,即b2+c2+bc=28,
∴(b+c)2-bc=28. ②
將①代入②,得(b+c)2-8=28,
∴b+c=6. 12分
考點:解三角形,正、余弦定理,面積公式


 海淀課時新作業金榜卷系列答案
海淀課時新作業金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 輕松課堂標準練系列答案
輕松課堂標準練系列答案科目:高中數學 來源: 題型:
| 3 |
| 3 |
| A、a=c |
| B、b=c |
| C、2a=c |
| D、a2+b2=c2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 11 | 14 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| b |
| a |
| sinB |
| cosA |
| 2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com