如果△A1B1C1的三個內角的余弦值分別等于△A2B2C2的三個內角的正弦值，則（ ）
A.△A1B1C1和△A2B2C2都是銳角三角形
B.△A1B1C1和△A2B2C2都是鈍角三角形
C.△A1B1C1是鈍角三角形，△A2B2C2是銳角三角形
D.△A1B1C1是銳角三角形，△A2B2C2是鈍角三角形
D
【解析】
試題分析：首先根據正弦、余弦在（0，π）內的符號特征，確定△A1B1C1是銳角三角形；
然后假設△A2B2C2是銳角三角形，則由cosα=sin（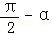
）推導出矛盾；
再假設△A2B2C2是直角三角形，易于推出矛盾；
最后得出△A2B2C2是鈍角三角形的結論．
【解析】
因為△A2B2C2的三個內角的正弦值均大于0，
所以△A1B1C1的三個內角的余弦值也均大于0，則△A1B1C1是銳角三角形．
若△A2B2C2是銳角三角形，由
，
得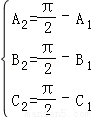
，
那么，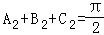
，這與三角形內角和是π相矛盾；
若△A2B2C2是直角三角形，不妨設A2=
，
則sinA2=1=cosA1，所以A1在（0，π）范圍內無值．
所以△A2B2C2是鈍角三角形．
故選D．
閱讀快車系列答案科目：高中數學 來源：[同步]2014新人教A版選修4-1 2.3圓的切線性質及判定定理練習（解析版） 題型：選擇題
（2009•崇文區一模）如圖，半徑相等的兩圓⊙O1，⊙O2相交于P，Q兩點．圓心O1在⊙O2上，PT是⊙O1的切線，PN是⊙O2的切線，則∠TPN的大小是（ ）
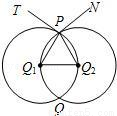
A.90° B.120° C.135° D.150°
查看答案和解析>>
科目：高中數學 來源：[同步]2014年蘇教版選修1-2 2.2直接證明與間接證明練習卷（解析版） 題型：選擇題
設a=lg2+lg5，b=ex（x＜0），則a與b大小關系為（ ）
A.a＞b B.a＜b C.a=b D.a≤b
查看答案和解析>>
科目：高中數學 來源：[同步]2014年蘇教版選修1-1 3.4導數在實際生活中的應用練習卷（解析版） 題型：填空題
做一個無蓋的圓柱形水桶，若要使體積是27π，且用料最省，則圓柱的底面半徑為 ．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
=（ ）
B.
C.
D.
的虛部是（ ）
B.
C.
D.
﹣
≥a+
﹣2．
的焦點坐標是 ．