
【題目】已知函數(shù)![]() (
(![]() ,
,![]() ).
).
(1)討論函數(shù)![]() 的單調(diào)性;
的單調(diào)性;
(2)當(dāng)![]() 時(shí),
時(shí),![]() ,求k的取值范圍.
,求k的取值范圍.
【答案】(1)詳見(jiàn)解析(2)![]() 或
或![]()
【解析】
(1)將函數(shù)求導(dǎo)并化簡(jiǎn),對(duì)![]() 分成
分成![]() 兩種情況,討論函數(shù)
兩種情況,討論函數(shù)![]() 的單調(diào)性.(2)原不等式即
的單調(diào)性.(2)原不等式即![]() (
(![]() ),當(dāng)
),當(dāng)![]() 時(shí),上述不等式顯然成立.當(dāng)
時(shí),上述不等式顯然成立.當(dāng)![]() 時(shí),將不等式變?yōu)?/span>
時(shí),將不等式變?yōu)?/span>![]() ,構(gòu)造函數(shù)
,構(gòu)造函數(shù)![]() ,利用導(dǎo)數(shù)研究函數(shù)的單調(diào)性,由此求得
,利用導(dǎo)數(shù)研究函數(shù)的單調(diào)性,由此求得![]() 的取值范圍.
的取值范圍.
解:(1)![]()
![]()
![]() .
.
①若![]() ,當(dāng)
,當(dāng)![]() 時(shí),
時(shí),![]() ,
,![]() 在
在![]() 上單調(diào)遞增;
上單調(diào)遞增;
當(dāng)![]() 時(shí),
時(shí),![]() ,
,![]() 在
在![]() 上單調(diào)遞減.
上單調(diào)遞減.
②若![]() ,當(dāng)
,當(dāng)![]() 時(shí),
時(shí),![]() ,
,![]() 在
在![]() 上單調(diào)遞減;
上單調(diào)遞減;
當(dāng)![]() 時(shí),
時(shí),![]() ,
,![]() 在
在![]() 上單調(diào)遞增.
上單調(diào)遞增.
∴當(dāng)![]() 時(shí),
時(shí),![]() 在
在![]() 上單調(diào)遞增,在
上單調(diào)遞增,在![]() 上單調(diào)遞減;
上單調(diào)遞減;
當(dāng)![]() 時(shí),
時(shí),![]() 在
在![]() 上單調(diào)遞減,在
上單調(diào)遞減,在![]() 上單調(diào)遞增.
上單調(diào)遞增.
(2)![]() (
(![]() ),
),
當(dāng)![]() 時(shí),上不等式成立,滿足題設(shè)條件;
時(shí),上不等式成立,滿足題設(shè)條件;
當(dāng)![]() 時(shí),
時(shí),![]() ,等價(jià)于
,等價(jià)于![]() ,
,
設(shè)![]() ,則
,則![]()
![]() ,
,
設(shè)![]() (
(![]() ),則
),則![]() ,
,
∴![]() 在
在![]() 上單調(diào)遞減,得
上單調(diào)遞減,得![]() .
.
①當(dāng)![]() ,即
,即![]() 時(shí),得
時(shí),得![]() ,
,![]() ,
,
∴![]() 在
在![]() 上單調(diào)遞減,得
上單調(diào)遞減,得![]() ,滿足題設(shè)條件;
,滿足題設(shè)條件;
②當(dāng)![]() ,即
,即![]() 時(shí),
時(shí),![]() ,而
,而![]() ,
,
∴![]() ,
,![]() ,又
,又![]() 單調(diào)遞減,
單調(diào)遞減,
∴當(dāng)![]() ,
,![]() ,得
,得![]() ,
,
∴![]() 在
在![]() 上單調(diào)遞增,得
上單調(diào)遞增,得![]() ,不滿足題設(shè)條件;
,不滿足題設(shè)條件;
綜上所述,![]() 或
或![]() .
.


 期末1卷素質(zhì)教育評(píng)估卷系列答案
期末1卷素質(zhì)教育評(píng)估卷系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在四棱錐![]() 中,
中,![]() ,
,![]() ,
,![]() ,且PC=BC=2AD=2CD=2
,且PC=BC=2AD=2CD=2![]() ,
,![]() .
.
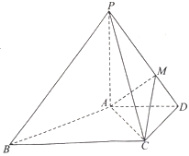
(1)![]() 平面
平面![]() ;
;
(2)已知點(diǎn)![]() 在線段
在線段![]() 上,且
上,且![]() ,求點(diǎn)
,求點(diǎn)![]() 到平面
到平面![]() 的距離.
的距離.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】給出以下四個(gè)說(shuō)法:
①回歸直線可以不過(guò)樣本的中心點(diǎn);
②在刻畫回歸模型的擬合效果時(shí),相關(guān)指數(shù)![]() 的值越大,說(shuō)明擬合的效果越好;
的值越大,說(shuō)明擬合的效果越好;
③在回歸直線方程![]() 中,當(dāng)解釋變量x每增加一個(gè)單位時(shí),預(yù)報(bào)變量
中,當(dāng)解釋變量x每增加一個(gè)單位時(shí),預(yù)報(bào)變量![]() 平均增加0.2個(gè)單位;
平均增加0.2個(gè)單位;
④對(duì)分類變量X與Y,若它們的隨機(jī)變量![]() 的觀測(cè)值k越小,則判斷“X與Y有關(guān)系”的把握程度越大.
的觀測(cè)值k越小,則判斷“X與Y有關(guān)系”的把握程度越大.
其中正確的說(shuō)法是( )
A.①④B.②③C.①③D.②③④
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】2019年9月23日,在![]() 省
省![]() 市舉辦的2019年中國(guó)農(nóng)民豐收節(jié)“新電商與農(nóng)業(yè)科技創(chuàng)新”論壇上,來(lái)自政府相關(guān)部門的領(lǐng)導(dǎo)及11所中國(guó)高校的專家學(xué)者以“農(nóng)業(yè)科技創(chuàng)新與鄉(xiāng)村振興”、“新農(nóng)人與脫貧攻堅(jiān)”為核心議題各抒己見(jiàn),農(nóng)產(chǎn)品方面的科技創(chuàng)新越來(lái)越成為21世紀(jì)大國(guó)崛起的一項(xiàng)重大突破.科學(xué)家對(duì)某農(nóng)產(chǎn)品每日平均增重量
市舉辦的2019年中國(guó)農(nóng)民豐收節(jié)“新電商與農(nóng)業(yè)科技創(chuàng)新”論壇上,來(lái)自政府相關(guān)部門的領(lǐng)導(dǎo)及11所中國(guó)高校的專家學(xué)者以“農(nóng)業(yè)科技創(chuàng)新與鄉(xiāng)村振興”、“新農(nóng)人與脫貧攻堅(jiān)”為核心議題各抒己見(jiàn),農(nóng)產(chǎn)品方面的科技創(chuàng)新越來(lái)越成為21世紀(jì)大國(guó)崛起的一項(xiàng)重大突破.科學(xué)家對(duì)某農(nóng)產(chǎn)品每日平均增重量![]() (單位:
(單位:![]() )與每日營(yíng)養(yǎng)液注射量
)與每日營(yíng)養(yǎng)液注射量![]() (單位:
(單位:![]() )之間的關(guān)系統(tǒng)計(jì)出表1一組數(shù)據(jù):
)之間的關(guān)系統(tǒng)計(jì)出表1一組數(shù)據(jù):
表1
| 1 | 2 | 3 | 4 | 5 |
| 2 | 3.5 | 5 | 6.6 | 8.4 |
(1)根據(jù)表1和表2的相關(guān)統(tǒng)計(jì)值求![]() 關(guān)于
關(guān)于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(2)計(jì)算擬合指數(shù)![]() 的值,并說(shuō)明線性回歸模型的擬合效果(
的值,并說(shuō)明線性回歸模型的擬合效果(![]() 的值在.98以上說(shuō)明擬合程度好);
的值在.98以上說(shuō)明擬合程度好);
(3)若某日該農(nóng)產(chǎn)品的營(yíng)養(yǎng)液注釋量為![]() ,預(yù)測(cè)該日這種農(nóng)產(chǎn)品的平均增長(zhǎng)重量(結(jié)果精確到0.1).
,預(yù)測(cè)該日這種農(nóng)產(chǎn)品的平均增長(zhǎng)重量(結(jié)果精確到0.1).
附:①
表2
|
|
|
|
92.4 | 55 | 25 | 0.04 |
②對(duì)于一組數(shù)據(jù)![]() ,
,![]() ,…,
,…,![]() ,其回歸線
,其回歸線![]() 的斜率和截距的最小二乘估計(jì)分別為:
的斜率和截距的最小二乘估計(jì)分別為: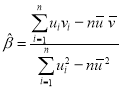 ,
,![]() ,
,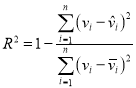 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某地有三家工廠,分別位于矩形ABCD的頂點(diǎn)A,B,及CD的中點(diǎn)P處,已知![]() km,
km,![]() ,為了處理三家工廠的污水,現(xiàn)要在矩形ABCD的區(qū)域上(含邊界),且A,B與等距離的一點(diǎn)O處建造一個(gè)污水處理廠,并鋪設(shè)排污管道AO,BO,OP,設(shè)排污管道的總長(zhǎng)為ykm.
,為了處理三家工廠的污水,現(xiàn)要在矩形ABCD的區(qū)域上(含邊界),且A,B與等距離的一點(diǎn)O處建造一個(gè)污水處理廠,并鋪設(shè)排污管道AO,BO,OP,設(shè)排污管道的總長(zhǎng)為ykm.
(I)按下列要求寫出函數(shù)關(guān)系式:
①設(shè)![]() ,將
,將![]() 表示成
表示成![]() 的函數(shù)關(guān)系式;
的函數(shù)關(guān)系式;
②設(shè)![]() ,將
,將![]() 表示成
表示成![]() 的函數(shù)關(guān)系式.
的函數(shù)關(guān)系式.
(Ⅱ)請(qǐng)你選用(I)中的一個(gè)函數(shù)關(guān)系式,確定污水處理廠的位置,使三條排水管道總長(zhǎng)度最短.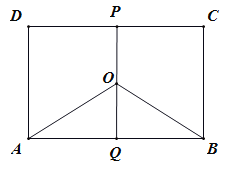
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知曲線C的參數(shù)方程為![]() (t為參數(shù)),以原點(diǎn)O為極點(diǎn),x軸的非負(fù)半軸為極軸建立極坐標(biāo)系,過(guò)極點(diǎn)的兩射線
(t為參數(shù)),以原點(diǎn)O為極點(diǎn),x軸的非負(fù)半軸為極軸建立極坐標(biāo)系,過(guò)極點(diǎn)的兩射線![]() 、
、![]() 相互垂直,與曲線C分別相交于A、B兩點(diǎn)(不同于點(diǎn)O),且
相互垂直,與曲線C分別相交于A、B兩點(diǎn)(不同于點(diǎn)O),且![]() 的傾斜角為銳角
的傾斜角為銳角![]() .
.
(1)求曲線C和射線![]() 的極坐標(biāo)方程;
的極坐標(biāo)方程;
(2)求△OAB的面積的最小值,并求此時(shí)![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() .
.
(1)求函數(shù)![]() 的單調(diào)遞減區(qū)間;
的單調(diào)遞減區(qū)間;
(2)求實(shí)數(shù)![]() 的值,使得
的值,使得![]() 是函數(shù)
是函數(shù)![]() 唯一的極值點(diǎn).
唯一的極值點(diǎn).
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() ,若關(guān)于
,若關(guān)于![]() 的方程
的方程![]() 恰有兩個(gè)不相等的實(shí)數(shù)根, 則實(shí)數(shù)
恰有兩個(gè)不相等的實(shí)數(shù)根, 則實(shí)數(shù)![]() 的取值范圍是
的取值范圍是![]()
![]()
A. ![]() B.
B. ![]() ,
,![]() C.
C. ![]() ,
,![]() D.
D. ![]() ,
,![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】下列說(shuō)法正確的個(gè)數(shù)是( )
①設(shè)某大學(xué)的女生體重![]() 與身高
與身高![]() 具有線性相關(guān)關(guān)系,根據(jù)一組樣本數(shù)據(jù)
具有線性相關(guān)關(guān)系,根據(jù)一組樣本數(shù)據(jù)![]() ,用最小二乘法建立的線性回歸方程為
,用最小二乘法建立的線性回歸方程為![]() ,則若該大學(xué)某女生身高增加
,則若該大學(xué)某女生身高增加![]() ,則其體重約增加
,則其體重約增加![]() ;
;
②關(guān)于![]() 的方程
的方程![]() 的兩根可分別作為橢圓和雙曲線的離心率;
的兩根可分別作為橢圓和雙曲線的離心率;
③過(guò)定圓![]() 上一定點(diǎn)
上一定點(diǎn)![]() 作圓的動(dòng)弦
作圓的動(dòng)弦![]() ,
,![]() 為原點(diǎn),若
為原點(diǎn),若![]() ,則動(dòng)點(diǎn)
,則動(dòng)點(diǎn)![]() 的軌跡為橢圓;
的軌跡為橢圓;
④已知![]() 是橢圓
是橢圓![]() 的左焦點(diǎn),設(shè)動(dòng)點(diǎn)
的左焦點(diǎn),設(shè)動(dòng)點(diǎn)![]() 在橢圓上,若直線
在橢圓上,若直線![]() 的斜率大于
的斜率大于![]() ,則直線
,則直線![]() (
(![]() 為原點(diǎn))的斜率的取值范圍是
為原點(diǎn))的斜率的取值范圍是![]() .
.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com