
【題目】如圖,在三棱柱![]() 中,點P,G分別是
中,點P,G分別是![]() ,
,![]() 的中點,已知
的中點,已知![]() ⊥平面ABC,
⊥平面ABC,![]() =
=![]() =3,
=3,![]() =
=![]() =2.
=2.
(I)求異面直線![]() 與AB所成角的余弦值;
與AB所成角的余弦值;
(II)求證:![]() ⊥平面
⊥平面![]() ;
;
(III)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.

【答案】(Ⅰ)![]() (Ⅱ)見解析(Ⅲ)
(Ⅱ)見解析(Ⅲ)![]()
【解析】分析:(Ⅰ)由題意得![]() ∥AB,故∠G
∥AB,故∠G![]() 是異面直線
是異面直線![]() 與AB所成的角,解三角形可得所求余弦值.(Ⅱ)在三棱柱
與AB所成的角,解三角形可得所求余弦值.(Ⅱ)在三棱柱![]() 中,由
中,由![]() ⊥平面ABC可得
⊥平面ABC可得![]() ⊥A1G,于是
⊥A1G,于是![]() ⊥A1G,又A1G⊥
⊥A1G,又A1G⊥![]() ,根據線面垂直的判定定理可得結論成立.(Ⅲ)取
,根據線面垂直的判定定理可得結論成立.(Ⅲ)取![]() 的中點H,連接AH,HG;取HG的中點O,連接OP,
的中點H,連接AH,HG;取HG的中點O,連接OP,![]() .由PO//A1G可得
.由PO//A1G可得![]() 平面
平面![]() ,
,
故得∠PC1O是PC1與平面![]() 所成的角,然后解三角形可得所求.
所成的角,然后解三角形可得所求.
詳解:
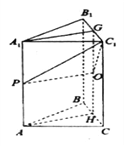
(I)∵![]() ∥AB,
∥AB,
∴∠G![]() 是異面直線
是異面直線![]() 與AB所成的角.
與AB所成的角.
∵![]() =
=![]() =2,G為BC的中點,
=2,G為BC的中點,
∴A1G⊥B1C1,
在![]() 中,
中,![]() ,
,
∴ ,
,
即異面直線AG與AB所成角的余炫值為![]() .
.
(II)在三棱柱![]() 中,
中,
∵![]() ⊥平面ABC,
⊥平面ABC,![]() 平面ABC,
平面ABC,
∴![]() ⊥A1G,
⊥A1G,
∴![]() ⊥A1G,
⊥A1G,
又A1G⊥![]() ,
,![]() ,
,
∴![]() 平面
平面![]() .
.
(III)解:取![]() 的中點H,連接AH,HG;取HG的中點O,連接OP,
的中點H,連接AH,HG;取HG的中點O,連接OP,![]() .
.
∵PO//A1G,
∴![]() 平面
平面![]() ,
,
∴∠PC1O是PC1與平面![]() 所成的角.
所成的角.
由已知得,![]() ,
,
∴![]()
∴直線![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() .
.


科目:高中數學 來源: 題型:
【題目】數學家歐拉在1765年發現,任意三角形的外心、重心、垂心位于同一條直線上,這條直線稱為歐拉線已知![]() 的頂點
的頂點![]() ,若其歐拉線的方程為
,若其歐拉線的方程為![]() ,則頂點
,則頂點![]() 的坐標為( )
的坐標為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設數列{an}的前n項和為Sn , 已知2Sn=3n+1+2n﹣3.
(1)求數列{an}的通項公式;
(2)求數列{nan}的前n項和Tn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=Asin(ωx+φ)(A>0,ω>0,|ω|< ![]() )的部分圖象如圖所示,下列說法正確的是( )
)的部分圖象如圖所示,下列說法正確的是( ) 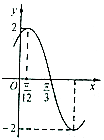
A.函數f(x)的最小正周期為2π
B.函數f(x)的圖象關于點(﹣ ![]() ,0)對稱
,0)對稱
C.將函數f(x)的圖象向左平移 ![]() 個單位得到的函數圖象關于y軸對稱
個單位得到的函數圖象關于y軸對稱
D.函數f(x)的單調遞增區間是[kπ+ ![]() ,kπ+
,kπ+ ![]() ](K∈Z)
](K∈Z)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若直線ax+by—4=0和圓x2+y2=4沒有公共點,則過點(a,b)的直線與橢圓![]() +
+![]() =1的公共點個數為( )
=1的公共點個數為( )
A. 0 B. 1 C. 2 D. 由a,b的取值來確定
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一動圓與定圓![]() 外切,同時和圓
外切,同時和圓![]() 內切,定點A(1,1).
內切,定點A(1,1).
(1)求動圓圓心P的軌跡E的方程,并說明是何種曲線;
(2)M為E上任意一點, F為E的左焦點,試求![]() 的最小值;
的最小值;
(3)試求![]() 的取值范圍;
的取值范圍;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,三角形ABC和梯形ACEF所在的平面互相垂直,AB⊥BC,AF⊥AC,AF ![]() 2CE,G是線段BF上一點,AB=AF=BC=2.
2CE,G是線段BF上一點,AB=AF=BC=2. 
(1)當GB=GF時,求證:EG∥平面ABC;
(2)求二面角E﹣BF﹣A的余弦值;
(3)是否存在點G滿足BF⊥平面AEG?并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com