
【題目】如圖,三角形ABC和梯形ACEF所在的平面互相垂直,AB⊥BC,AF⊥AC,AF ![]() 2CE,G是線段BF上一點,AB=AF=BC=2.
2CE,G是線段BF上一點,AB=AF=BC=2. 
(1)當GB=GF時,求證:EG∥平面ABC;
(2)求二面角E﹣BF﹣A的余弦值;
(3)是否存在點G滿足BF⊥平面AEG?并說明理由.
【答案】
(1)證明:取AB中點D,連接GD,CD,

又GB=GF,所以 ![]() .
.
因為 ![]() ,所以
,所以 ![]() ,四邊形GDCE是平行四邊形,
,四邊形GDCE是平行四邊形,
所以CD∥EG
因為EG平面ABC,CD平面ABC
所以EG∥平面ABC.
(2)解:因為平面ABC⊥平面ACEF,平面ABC∩平面ACEF=AC,
且AF⊥AC,所以AF⊥平面ABC,
所以AF⊥AB,AF⊥BC
因為BC⊥AB,所以BC⊥平面ABF.
如圖,以A為原點,建立空間直角坐標系A﹣xyz.

則F(0,0,2),B(2,0,0),C(2,2,0),E(2,2,1), ![]() 是平面ABF的一個法向量.
是平面ABF的一個法向量.
設平面BEF的法向量n=(x,y,z),則  ,即
,即 ![]()
令y=1,則z=﹣2,x=﹣2,所以n=(﹣2,1,﹣2),所以  ,
,
由題知二面角E﹣BF﹣A為鈍角,所以二面角E﹣BF﹣A的余弦值為 ![]() .
.
(3)解:因為 ![]() ,所以BF與AE不垂直,
,所以BF與AE不垂直,
所以不存在點G滿足BF⊥平面AEG.
【解析】(1)當GB=GF時,根據線面平行的判定定理即可證明EG∥平面ABC;(2)建立空間直角坐標系,利用向量法即可求二面角E﹣BF﹣A的余弦值;(3)根據線面垂直的判定定理和性質定理,建立條件關系即可得到結論.
【考點精析】本題主要考查了直線與平面平行的判定和直線與平面垂直的判定的相關知識點,需要掌握平面外一條直線與此平面內的一條直線平行,則該直線與此平面平行;簡記為:線線平行,則線面平行;一條直線與一個平面內的兩條相交直線都垂直,則該直線與此平面垂直;注意點:a)定理中的“兩條相交直線”這一條件不可忽視;b)定理體現了“直線與平面垂直”與“直線與直線垂直”互相轉化的數學思想才能正確解答此題.


 字詞句篇與同步作文達標系列答案
字詞句篇與同步作文達標系列答案科目:高中數學 來源: 題型:
【題目】如圖,在三棱柱![]() 中,點P,G分別是
中,點P,G分別是![]() ,
,![]() 的中點,已知
的中點,已知![]() ⊥平面ABC,
⊥平面ABC,![]() =
=![]() =3,
=3,![]() =
=![]() =2.
=2.
(I)求異面直線![]() 與AB所成角的余弦值;
與AB所成角的余弦值;
(II)求證:![]() ⊥平面
⊥平面![]() ;
;
(III)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.

查看答案和解析>>
科目:高中數學 來源: 題型:
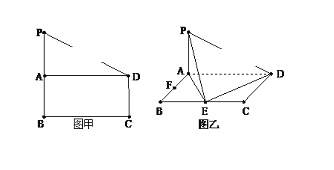
【題目】如圖甲,在直角梯形PBCD中,PB∥CD,CD⊥BC,BC=PB=2CD,A是PB的中點.
現沿AD把平面PAD折起,使得PA⊥AB(如圖乙所示),E、F分別為BC、AB邊的中點.
(1)求證:平面PAE⊥平面PDE;
(2)在PE上找一點Q,使得平面BDQ⊥平面ABCD.
(3)在PA上找一點G,使得FG∥平面PDE.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設P是不等式組  表示的平面區域內的任意一點,向量
表示的平面區域內的任意一點,向量 ![]() =(1,1),
=(1,1), ![]() =(2,1),若
=(2,1),若 ![]() =λ
=λ ![]() +μ
+μ ![]() (λ,μ為實數),則λ﹣μ的最大值為( )
(λ,μ為實數),則λ﹣μ的最大值為( )
A.4
B.3
C.﹣1
D.﹣2
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】連接球面上兩點的線段稱為球的弦,半徑為4的球的兩條弦AB,CD的長度分別為2 ![]() 和4
和4 ![]() ,M,N分別是AB,CD的中點,兩條弦的兩端都在球面上運動,有下面四個命題:
,M,N分別是AB,CD的中點,兩條弦的兩端都在球面上運動,有下面四個命題:
①弦AB,CD可能相交于點M;
②弦AB,CD可能相交于點N;
③MN的最大值是5;
④MN的最小值是1;
其中所有正確命題的序號為 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設p:實數x滿足x2-2(a+1)x+2a+a2<0,q:實數x滿足![]()
(1)若a=1,且p∧q為真,求實數x的取值范圍;
(2)若p是q的必要不充分條件,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在下列結論中:
①若向量![]() 共線,則向量
共線,則向量![]() 所在的直線平行;
所在的直線平行;
②若向量![]() 所在的直線為異面直線,則向量
所在的直線為異面直線,則向量![]() 一定不共面;
一定不共面;
③若三個向量![]() 兩兩共面,則向量
兩兩共面,則向量![]() 共面;
共面;
④已知空間的三個向量![]() ,則對于空間的任意一個向量
,則對于空間的任意一個向量![]() 總存在實數x,y,z使得
總存在實數x,y,z使得![]() .
.
其中正確結論的個數是( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() ,曲線f(x)=
,曲線f(x)= ![]() 在點(e,f(e))處的切線與直線e2x﹣y+e=0垂直.(注:e為自然對數的底數) (Ⅰ)若函數f(x)在區間(m,m+1)上存在極值,求實數m的取值范圍;
在點(e,f(e))處的切線與直線e2x﹣y+e=0垂直.(注:e為自然對數的底數) (Ⅰ)若函數f(x)在區間(m,m+1)上存在極值,求實數m的取值范圍;
(Ⅱ)求證:當x>1時, ![]() >
> ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設集合A={x|﹣1≤x≤2},B={x|x2﹣x+(m﹣m2)<0}.
(1)當m< ![]() 時,化簡集合B;
時,化簡集合B;
(2)p:x∈A,命題q:x∈B,且命題p是命題q的必要不充分條件,求實數m的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com