
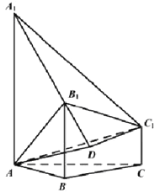
【題目】已知多面體![]() ,
,![]() ,
,![]() ,
,![]() 均垂直于平面
均垂直于平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)證明:![]() ⊥平面
⊥平面![]() ;
;
(2)求直線![]() 與平面
與平面![]() 所成的角的正弦值.
所成的角的正弦值.
【答案】(1)見解析;(2)直線![]() 與平面
與平面![]() 所成的角的正弦值為
所成的角的正弦值為![]() .
.
【解析】
(1)根據(jù)直線與平面垂直的判定定理,要證![]() 平面
平面![]() ,只需證
,只需證![]() 與平面
與平面![]() 兩條相交直線垂直。根據(jù)已知條件可求
兩條相交直線垂直。根據(jù)已知條件可求![]() 與
與![]() 的長度,然后跟據(jù)勾股定理可證
的長度,然后跟據(jù)勾股定理可證![]() .。同理可得
.。同理可得![]() .,進(jìn)而可得
.,進(jìn)而可得![]() 平面
平面![]() 。(2)要求直線
。(2)要求直線![]() 與平面
與平面![]() 所成的角的正弦值,應(yīng)先作角。由條件可得平面
所成的角的正弦值,應(yīng)先作角。由條件可得平面![]() 平面
平面![]() 。所以過點(diǎn)
。所以過點(diǎn)![]() 作
作![]() ,交直線
,交直線![]() 于點(diǎn)
于點(diǎn)![]() ,連結(jié)
,連結(jié)![]() . 可知
. 可知![]() 是
是![]() 與平面
與平面![]() 所成的角.根據(jù)條件可求
所成的角.根據(jù)條件可求![]() 的三邊長,進(jìn)而可由余弦定理求得
的三邊長,進(jìn)而可由余弦定理求得![]() ,然后可求
,然后可求![]() 。進(jìn)而求得
。進(jìn)而求得![]() ,在
,在![]() 中即可求得結(jié)果。
中即可求得結(jié)果。
(1)由![]() 得
得![]() ,
,
所以![]() .
.
故![]() .
.
由![]() ,
,![]()
![]() 得
得![]() ,
,
由![]() 得
得![]() ,
,
由![]() ,得
,得![]() ,所以
,所以![]() ,故
,故![]() .
.
因此![]() 平面
平面![]() .
.
(2)如圖,過點(diǎn)![]() 作
作![]() ,交直線
,交直線![]() 于點(diǎn)
于點(diǎn)![]() ,連結(jié)
,連結(jié)![]() .
.
由![]() 平面
平面![]() 得平面
得平面![]() 平面
平面![]() ,
,
由![]() 得
得![]() 平面
平面![]() ,
,
所以![]() 是
是![]() 與平面
與平面![]() 所成的角.
所成的角.
由![]() 得
得![]() ,
,
所以![]() ,故
,故![]() .
.
因此,直線![]() 與平面
與平面![]() 所成的角的正弦值是
所成的角的正弦值是![]() .
.
方法二:
(1)如圖,以AC的中點(diǎn)O為原點(diǎn),分別以射線OB,OC為x,y軸的正半軸,建立空間直角坐標(biāo)系O-xyz.
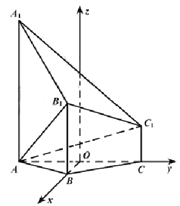
由題意知各點(diǎn)坐標(biāo)如下:![]()
因此![]()
由![]() 得
得![]() .
.
由![]() 得
得![]() .
.
所以![]() 平面
平面![]() .
.
(2)設(shè)直線![]() 與平面
與平面![]() 所成的角為
所成的角為![]() .
.
由(Ⅰ)可知![]()
設(shè)平面![]() 的法向量
的法向量![]() .
.
由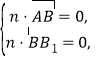 即
即![]() 可取
可取![]() .
.
所以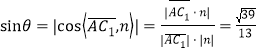 .
.
因此,直線![]() 與平面
與平面![]() 所成的角的正弦值是
所成的角的正弦值是![]() .
.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知以點(diǎn)A(-1,2)為圓心的圓與直線l1:x+2y+7=0相切.過點(diǎn)B(-2,0)的動(dòng)直線l與圓A相交于M,N兩點(diǎn).
(1)求圓A的方程;
(2)當(dāng)|MN|=2時(shí),求直線l的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在三棱柱![]() 中,點(diǎn)P,G分別是
中,點(diǎn)P,G分別是![]() ,
,![]() 的中點(diǎn),已知
的中點(diǎn),已知![]() ⊥平面ABC,
⊥平面ABC,![]() =
=![]() =3,
=3,![]() =
=![]() =2.
=2.
(I)求異面直線![]() 與AB所成角的余弦值;
與AB所成角的余弦值;
(II)求證:![]() ⊥平面
⊥平面![]() ;
;
(III)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知命題![]() :實(shí)數(shù)
:實(shí)數(shù)![]() 滿足
滿足![]() ,
,![]() :實(shí)數(shù)
:實(shí)數(shù)![]() 滿足
滿足![]()
(1)若![]() 為真命題,求實(shí)數(shù)
為真命題,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
(2)若![]() 是
是![]() 的充分不必要條件,求實(shí)數(shù)
的充分不必要條件,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知等差數(shù)列的前三項(xiàng)依次為a,3,5a,前n項(xiàng)和為Sn,且Sk=121.
(1)求a及k的值;
(2)設(shè)數(shù)列{bn}的通項(xiàng)bn=![]() ,證明數(shù)列{bn}是等差數(shù)列,并求其前n項(xiàng)和Tn.
,證明數(shù)列{bn}是等差數(shù)列,并求其前n項(xiàng)和Tn.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】(本小題滿分12分)
如圖,在四棱錐P—ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AP=AB,BP=BC=2,E,F分別是PB,PC的中點(diǎn).
(Ⅰ)證明:EF∥平面PAD;
(Ⅱ)求三棱錐E—ABC的體積V.

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖甲,在直角梯形PBCD中,PB∥CD,CD⊥BC,BC=PB=2CD,A是PB的中點(diǎn).
現(xiàn)沿AD把平面PAD折起,使得PA⊥AB(如圖乙所示),E、F分別為BC、AB邊的中點(diǎn).
(1)求證:平面PAE⊥平面PDE;
(2)在PE上找一點(diǎn)Q,使得平面BDQ⊥平面ABCD.
(3)在PA上找一點(diǎn)G,使得FG∥平面PDE.
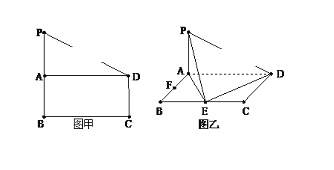
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)P是不等式組  表示的平面區(qū)域內(nèi)的任意一點(diǎn),向量
表示的平面區(qū)域內(nèi)的任意一點(diǎn),向量 ![]() =(1,1),
=(1,1), ![]() =(2,1),若
=(2,1),若 ![]() =λ
=λ ![]() +μ
+μ ![]() (λ,μ為實(shí)數(shù)),則λ﹣μ的最大值為( )
(λ,μ為實(shí)數(shù)),則λ﹣μ的最大值為( )
A.4
B.3
C.﹣1
D.﹣2
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)= ![]() ,曲線f(x)=
,曲線f(x)= ![]() 在點(diǎn)(e,f(e))處的切線與直線e2x﹣y+e=0垂直.(注:e為自然對數(shù)的底數(shù)) (Ⅰ)若函數(shù)f(x)在區(qū)間(m,m+1)上存在極值,求實(shí)數(shù)m的取值范圍;
在點(diǎn)(e,f(e))處的切線與直線e2x﹣y+e=0垂直.(注:e為自然對數(shù)的底數(shù)) (Ⅰ)若函數(shù)f(x)在區(qū)間(m,m+1)上存在極值,求實(shí)數(shù)m的取值范圍;
(Ⅱ)求證:當(dāng)x>1時(shí), ![]() >
> ![]() .
.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com