
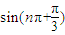 ,②
,②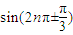 ,③
,③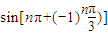 ,④
,④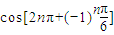 中,與sin
中,與sin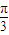 相等的是( )
相等的是( ) 激活思維智能訓練課時導學練系列答案
激活思維智能訓練課時導學練系列答案科目:高中數學 來源: 題型:
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
| A、①和② | B、③和④ |
| C、①和④ | D、②和③ |
查看答案和解析>>
科目:高中數學 來源: 題型:
| -2x+b |
| 2x+1+a |
| 3 |
| 2 |
| 5 |
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| k |
| 2 |
| 17 |
| 8 |
查看答案和解析>>
科目:高中數學 來源:學習周報 數學 北師大課標高一版(必修4) 2009-2010學年 第41期 總197期 北師大課標版 題型:013
若n∈Z,則在①sin![]() ;②sin
;②sin![]() ;③sin
;③sin![]() 中與sin
中與sin![]() 相等的是
相等的是
①和②
①和③
②
③
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com