
(I)證明:當![]() 時,
時,![]() 在
在![]() 上是增函數;
上是增函數;
(II)對于給定的閉區間![]() ,試說明存在實數
,試說明存在實數 ![]() ,當
,當![]() 時,
時,![]() 在閉區間
在閉區間![]() 上是減函數;
上是減函數;
(III)證明:![]() .
.
(I)證明:由題設得g(x)=e2x-t(ex+1)+x,![]() (x)=2e2x-tex+1.
(x)=2e2x-tex+1.
又由2ex+e-x≥2![]() ,且t<2
,且t<2![]() 得t<2ex+e-x,即
得t<2ex+e-x,即
![]() (x)=2e2x-tex+1>0.
(x)=2e2x-tex+1>0.
由此可知,g(x)為R上的增函數.
(II)證法一:因為![]() (x)<0是g(x)為減函數的充分條件,所以只要找到實數k,使得t>k時,在閉區間[a,b]上成立即可.
(x)<0是g(x)為減函數的充分條件,所以只要找到實數k,使得t>k時,在閉區間[a,b]上成立即可.
因為y=2ex+e-x在閉區間[a,b]上連續,故在閉區間[a,b]上有最大值,設其為k,于是在t>k時,![]() (x)<0在閉區間[a,b]上恒成立,即g(x)在閉區間[a,b]上為減函數.
(x)<0在閉區間[a,b]上恒成立,即g(x)在閉區間[a,b]上為減函數.
證法二:因為![]() (x)<0是g(x)為減函數的充分條件,所以只要找到實數k,使得t>k時,
(x)<0是g(x)為減函數的充分條件,所以只要找到實數k,使得t>k時,
![]() (x)=2e2x-tex+1<0,
(x)=2e2x-tex+1<0,
在閉區間[a,b]上成立即可.
令m=ex,則![]() (x)<0(x∈[a,b])當且僅當
(x)<0(x∈[a,b])當且僅當
2m2-tm+1<0(m∈[ea,eb]).
而上式成立只需要

成立.取2ea+e-a與2eb+e-b中較大者記為k,易知當t>k, ![]() (x)<0在閉區間[a,b]上恒成立,即g(x)在閉區間[a,b]上為減函數.
(x)<0在閉區間[a,b]上恒成立,即g(x)在閉區間[a,b]上為減函數.
(III)證法一:設F(t)=2t2-2(ex+x)t+e2x+x2+1,即
F(t)=2![]()
易得
F(t)≥![]() (ex-x)2+1.
(ex-x)2+1.
令H(x)=ex-x,則![]() (x)=ex-1,易知
(x)=ex-1,易知![]() (0)=0.當x>0時.
(0)=0.當x>0時.![]() (x)>0;當x<0時,
(x)>0;當x<0時,![]() (x)<0.故當x=0時,H(x)取最小值,H(0)=1.所以
(x)<0.故當x=0時,H(x)取最小值,H(0)=1.所以
![]()
于是對任意x、t,有F(t)≥![]() ,即f(x) ≥
,即f(x) ≥![]() .
.
證法二:設F(t)=2t2-2(ex+x)t+e2x+x2+1,
F(x)≥![]() 當且僅當
當且僅當
2t2-2(ex+x)t+e2x+x2-![]() ≥0.
≥0.
只需證明
4(ex+x)2-2×4(e2x-x2-![]() )≤0,
)≤0,
即
(ex-x)2≥1.
以下同證法一
證法三:設F(t)=2t2-2(ex+x)t+e2x+x2+1,則
F′(t)=4t-2(ex+x).
易得F′(![]() )=0。當t>
)=0。當t>![]() 時,F′(t)>0;當t<
時,F′(t)>0;當t<![]() 時,F′(t)<0,故當t=
時,F′(t)<0,故當t=![]() 時,F(t)取最小值
時,F(t)取最小值![]()
F(t)≥![]() ( ex-x)2+1.
( ex-x)2+1.
以下同證法一.
證法四:f(x)=(ex-t)2+(x-t)2+1.
設點A、B的坐標分別為(x,ex)、(t,t),易知點B在直線y=x上,令點A到直線y=x的距離為d,則
f(x)=|AB|2+1≥d2+1=![]() (ex-x)2+1.
(ex-x)2+1.
以下同證法一.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源:2010-2011年遼寧省瓦房店市高級中學高二下學期期末聯考理科數學 題型:解答題
(本題滿分12分)
已知函數 .
.
(I)若函數 在
在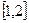 上是減函數,求實數
上是減函數,求實數 的取值范圍;
的取值范圍;
(II)令 ,是否存在實數
,是否存在實數 ,使得當
,使得當 時,函數
時,函數 的最小值是
的最小值是 ,若存在,求出實數
,若存在,求出實數 的值,若不存在,說明理由?
的值,若不存在,說明理由?
(III)當 時,證明:
時,證明: .
.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年內蒙古巴彥淖爾市高三第一學期期中考試理科數學 題型:解答題
(本題滿分12分)已知函數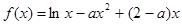 .
.
(I)討論 的單調性;
的單調性;
(II)設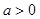 ,證明:當
,證明:當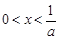 時,
時,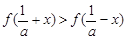 ;
;
(III)若函數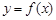 的圖像與x軸交于A,B兩點,線段AB中點的橫坐標為x0,證明:
的圖像與x軸交于A,B兩點,線段AB中點的橫坐標為x0,證明: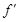 (x0)<0.
(x0)<0.
查看答案和解析>>
科目:高中數學 來源:2011年河北省高一上學期期中考試數學 題型:解答題
本小題滿分12分)
已知函數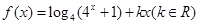 是偶函數.
是偶函數.
(I)證明:對任意實數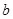 ,函數
,函數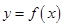 的圖象與直線
的圖象與直線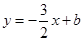 最多只有一個交點;
最多只有一個交點;
(II)若方程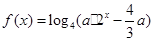 有且只有一個解,求實數
有且只有一個解,求實數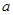 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2010-2011年遼寧省瓦房店市高二下學期期末聯考理科數學 題型:解答題
(本題滿分12分)
已知函數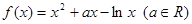 .
.
(I)若函數 在
在 上是減函數,求實數
上是減函數,求實數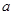 的取值范圍;
的取值范圍;
(II)令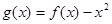 ,是否存在實數
,是否存在實數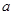 ,使得當
,使得當 時,函數
時,函數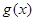 的最小值是
的最小值是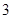 ,若存在,求出實數
,若存在,求出實數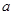 的值,若不存在,說明理由?
的值,若不存在,說明理由?
(III)當 時,證明:
時,證明: .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com