
【題目】已知點 A(a , b),拋物線C :![]() (a ≠0 , b ≠0 , a ≠2p).過點 A 作直線l ,交拋物線 C 于點P 、Q .如果以線段 PQ 為直徑的圓過拋物線C 的頂點,求直線 l 的方程
(a ≠0 , b ≠0 , a ≠2p).過點 A 作直線l ,交拋物線 C 于點P 、Q .如果以線段 PQ 為直徑的圓過拋物線C 的頂點,求直線 l 的方程
【答案】bx -(a -2p)y -2bp =0 或![]() .
.
【解析】
1.如果直線 l 過原點, 顯然滿足要求, 此時方程為![]() .
.
2.如果直線 l 不過原點, 設其方程為x = m(y - b) + a .
又設 P(x1 , y1)、Q(x2 , y2), 則OP ⊥OQ![]() .
.
因為![]() , 所以,
, 所以,![]() .
.
由方程組![]() 消去x得
消去x得![]() . ①
. ①
由韋達定理得![]() .
.
所以,![]() .
.
故所求方程為bx -(a -2p)y -2bp =0 . ②
由于-4p2 < 0 , 所以, -2p(a - bm)< 0, 即方程①的常數項為負 .
從而, 判別式大于 0, 方程 ①一定有解 y1、y2.故方程②符合題意.
綜上直線 l 的方程為![]() 或bx -(a -2p)y -2bp =0 .
或bx -(a -2p)y -2bp =0 .


 優百分課時互動系列答案
優百分課時互動系列答案 開心蛙狀元作業系列答案
開心蛙狀元作業系列答案 課時掌控隨堂練習系列答案
課時掌控隨堂練習系列答案科目:高中數學 來源: 題型:
【題目】在四棱錐![]() 中,側面
中,側面![]() ⊥底面
⊥底面![]() ,底面
,底面![]() 為直角梯形,
為直角梯形,![]() //
//![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 為
為![]() 的中點.
的中點.

(Ⅰ)求證:PA//平面BEF;
(Ⅱ)若PC與AB所成角為![]() ,求
,求![]() 的長;
的長;
(Ⅲ)在(Ⅱ)的條件下,求二面角F-BE-A的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知過拋物線![]() 的焦點
的焦點![]() ,斜率為
,斜率為![]() 的直線交拋物線于
的直線交拋物線于![]() 兩點,且
兩點,且![]() .
.
(1)求該拋物線![]() 的方程;
的方程;
(2)已知拋物線上一點![]() ,過點
,過點![]() 作拋物線的兩條弦
作拋物線的兩條弦![]() 和
和![]() ,且
,且![]() ,判斷直線
,判斷直線![]() 是否過定點?并說明理由.
是否過定點?并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】據權威部門統計,高中學生眼睛近視已是普遍現象,這與每個學生是否科學用眼有很大關系.每年5月5日是全國愛眼日,我市某中學在此期間開展了一系列的用眼衛生教育活動.為了解本校學生用眼衛生情況,學校醫務室隨機抽取了100名學生對其進行調查,下面是根據調查結果繪制的學生不間斷用眼時間(單位:分鐘)的頻率分布直方圖,且將不間斷用眼時間不低于60分鐘的學生稱為“不愛護眼者”,低于60分鐘的學生稱為“愛護眼者”.
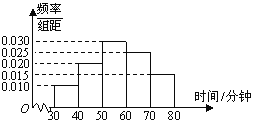
(1)根據頻率分布直方圖,求這100名學生不間斷用眼時間的平均數和中位數(結果精確到0.1);
(2)根據已知條件完成下面2×2列聯表,并據此判斷是否有99%的把握認為“不愛護眼者”與性別有關?
愛護眼者 | 不愛護眼者 | 合計 | |
男 | 45 | ||
女 | 15 | ||
合計 |
(3)在不間斷用眼時間為![]() 和
和![]() 兩組人中先按分層抽樣的方法任意選取5人,再從這5人中隨機抽取2人了解他們的視力狀況,求這兩人來自不同組別的概率.
兩組人中先按分層抽樣的方法任意選取5人,再從這5人中隨機抽取2人了解他們的視力狀況,求這兩人來自不同組別的概率.
附:![]()
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,某地出土的一種“釘”是由四條線段組成,其結構能使它任意拋至水平面后,總有一端所在的直線豎直向上,并記組成該“釘”的四條線段的公共點為O,釘尖為![]() .
.
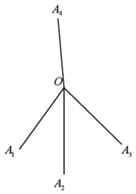
⑴設![]() ,當
,當![]() ,
,![]() ,
,![]() 在同一水平面內時,求
在同一水平面內時,求![]() 與平面
與平面![]() 所成角的大小
所成角的大小![]() 結果用反三角函數值表示
結果用反三角函數值表示![]() .
.
⑵若該“釘”的三個釘尖所確定的三角形的面積為![]() ,要用某種線型材料復制100枚這種“釘”
,要用某種線型材料復制100枚這種“釘”![]() 損耗忽略不計
損耗忽略不計![]() ,共需要該種材料多少米?
,共需要該種材料多少米?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com