Question

已知異面直線a、b成60°角，過空間一點p，與a、b也都成60°角的直線，可以作（ ）
A．1條
B．2條
C．3條
D．4條

Answer 1

【答案】分析：作出過P與a、b分別平行的兩條直線a'、b'，則a'、b'所成銳角即為異面直線a、b所成角．設直線a'、b'確定的平面為α，通過討論可知：在平面α內有一條直線與a'、b'都成60°角，在平面α外有兩條直線與a'、b'都成60°角．最后結合異面直線所成角的定義，即可得到過點P與a、b也都成60°的角直線可以作3條．
解答：解：過P作a'∥a，b'∥b，設直線a'、b'確定的平面為α
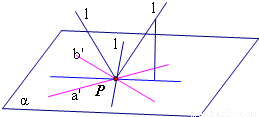
∵異面直線a、b成60°角，∴直線a'、b'所成銳角為60°
①當直線l在平面α內時，若直線l平分直線a'、b'所成的鈍角，
則直線l與a、b都成60°角；
②當直線l與平面α斜交時，若它在平面α內的射影恰好落在
直線a'、b'所成的銳角平分線上時，直線l與a、b所成角相等．
此時l與a'、b'所成角的范圍為[30°，90°]，適當調整l的位置，可使直線l與a、b也都成60°角，這樣的直線l有兩條．
綜上所述，過點P與a'、b'都成60°角的直線，可以作3條
∵a'∥a，b'∥b，
∴過點P與a'、b'都成60°角的直線，與a、b也都成60°的角．
故選C
點評：本題給出兩條異面直線的所成角，要我們找出與它們成60度角的第三條直線有幾條，著重考查了線面垂直、直線與平面所成角和異面直線所成角等知識，屬于基礎題．