
(本小題滿分12分)已知數列{an}滿足an=2an-1+2n+1(n∈N,n>1),a3=27,數列{bn}滿足bn= (an+t).
(an+t).
(1)若數列{bn}為等差數列,求bn;
(2)在(1)的條件下,求數列{an}的前n項和Sn.
(1)bn=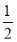 +n;(2)Sn=(2n-1)×2n-n+1
+n;(2)Sn=(2n-1)×2n-n+1
【解析】
試題分析:(1)利用{bn}成等差數列,先求出t的值,進而得到b1和公差,即可求得通項公式;(2)根據(1),可以求出{an}的通項公式,然后利用錯位相減法可求出Sn.
試題解析:(1)由a3=27,得27=2a2+23+1,于是a2=9
∴9=2a1+22+1,∴a1=2
于是b1= (2+t),b2=
(2+t),b2=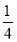 (9+t),b3=
(9+t),b3=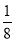 (27+t)
(27+t)
∵{bn}成等差數列,故2b2=b1+b3
即2×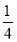 (9+t)=
(9+t)= (2+t)+
(2+t)+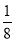 (27+t)
(27+t)
解得t=1,∴b1=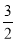 ,b2=
,b2=
bn-bn-1=1=d
∴bn=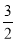 +(n-1)=
+(n-1)= +n(n∈N*)
+n(n∈N*)
(2)∵bn=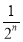 (an+1)=
(an+1)= +n
+n
∴an=(n+ )·2n-1=(2n-1)·2n-1-1
)·2n-1=(2n-1)·2n-1-1
∴Sn=(3×20-1)+(5×21-1)+(7×22-1)+……+[(2n+1)×2n-1-1]
=3×20+5×21+7×22+……+(2n+1)×2n-1-n
2Sn= 3×21+5×22+7×23+……+(2n+1)×2n-n
作差:-Sn=3+2×2+2×22+2×23+……+2×2n-1-(2n+1)×2n+n
=1+2× -(2n+1)×2n+n
-(2n+1)×2n+n
=(1-2n)×2n+n-1
∴Sn=(2n-1)×2n-n+1(n∈N*)
考點:等差數列,遞推數列,通項公式,數列的前n項和,錯位相減法求和


 字詞句段篇系列答案
字詞句段篇系列答案科目:高中數學 來源:2015屆四川省成都實驗外國語高三11月月考文科數學試卷(解析版) 題型:填空題
若數列 滿足:存在正整數
滿足:存在正整數 ,對于任意正整數
,對于任意正整數 都有
都有 成立,則稱數列
成立,則稱數列 為周期數列,周期為
為周期數列,周期為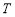 . 已知數列
. 已知數列 滿足
滿足 ,
,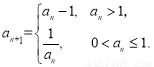 現給出以下命題:
現給出以下命題:
①若 ,則
,則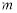 可以取3個不同的值
可以取3個不同的值
②若 ,則數列
,則數列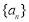 是周期為
是周期為 的數列
的數列
③ 且
且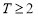 ,存在
,存在 ,
, 是周期為
是周期為 的數列
的數列
④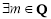 且
且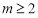 ,數列
,數列 是周期數列.其中所有真命題的序號是 .
是周期數列.其中所有真命題的序號是 .
查看答案和解析>>
科目:高中數學 來源:2015屆四川省高三10月月考文科數學試卷(解析版) 題型:選擇題
用C(A)表示非空集合A中的元素個數,定義A*B=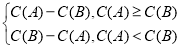 .若A={1,2},
.若A={1,2},
B=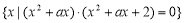 ,且A*B=1,設實數
,且A*B=1,設實數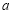 的所有可能取值集合是S,則C(S)=( )
的所有可能取值集合是S,則C(S)=( )
A.4 B.3 C.2 D.1
查看答案和解析>>
科目:高中數學 來源:2015屆四川省高三10月月考文科數學試卷(解析版) 題型:選擇題
為了得到函數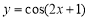 的圖象,只需將函數
的圖象,只需將函數 的圖象上所有的點( )
的圖象上所有的點( )
A.向左平移 個單位長度
個單位長度
B.向右平移 個單位長度
個單位長度
C.向左平移1個單位長度
D.向右平移1個單位長度
查看答案和解析>>
科目:高中數學 來源:2015屆四川省巴蜀好教育聯盟12月大聯考理科數學試卷(解析版) 題型:選擇題
從0,1,3,4,5,6六個數字中,選出一個偶數和兩個奇數,組成一個沒有重復數字的三位數,這樣的三位數共有( )
A、24個 B、36個 C、48個 D、54個
查看答案和解析>>
科目:高中數學 來源:2015屆四川省巴蜀好教育聯盟12月大聯考文科數學試卷(解析版) 題型:選擇題
函數f(x)是定義在R上的偶函數,且滿足f(x+2)=f(x),當x∈[0,1]時,f(x)=2x,若方程ax+a-f(x)=0(a>0)恰有三個不相等的實數根,則實數a的取值范圍是( )
A、(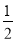 ,1) B、[0,2] C、(1,2) D、[1,+∞)
,1) B、[0,2] C、(1,2) D、[1,+∞)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com