【題目】已知函數
.
（1）討論函數
的單調性；
（2）討論函數的零點個數.
【答案】（1）當
時，
在
上單調遞增，當
時，在
）上單調遞減，在
上單調遞增；（2）當
或
時，有1個零點；當
時，有2個零點；當
時，有0個零點.
【解析】
（1）對函數求導，分類討論和時的單調性，即可得到結果.
（2）
不是的零點，即可分類參量，求解
的交點個數問題，對新函數
求導后作圖，進而計算出零點個數問題.
（1）的定義域為，
，
當時，
所以在上單調遞增，
當時，由
得
，
所以
，
，單調遞減，
，，單調遞增 ，
綜上，當時，在上單調遞增，
當時，在）上單調遞減，在上單調遞增；
（2）顯然不是的零點，
當
時，由
得，
令，則
.
所以
在
上單調遞減，
上單調遞減，
上單調遞增，
且當
時，
，當x從左邊趨近于0時，
，當x從右邊趨近于0時，
，畫出的圖象如圖，數形結合知，
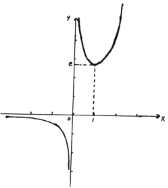
當
或
即或時，有1個零點，
當
即時，有2個零點，
當
即時，有0個零點.
科目：高中數學 來源： 題型：
【題目】在直角坐標系
中，以坐標原點為極點，
軸正半軸為極軸建立極坐標系，曲線
的極坐標方程為
.
為曲線上的動點，點
在射線
上，且滿足
.
（Ⅰ）求點的軌跡
的直角坐標方程；
（Ⅱ）設與軸交于點
，過點且傾斜角為
的直線
與相交于
兩點，求
的值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】將420名工人編號為：001，002，
，420，采用系統抽樣的方法抽取一個容量為60的樣本，且隨機抽得的號碼為005．這420名工人來自三個工廠，從001到200為
工廠，從201到355為
工廠，從356到420為
工廠，則三個工廠被抽中的工人數依次為（ ）
A.28，23，9B.27，23，10C.27，22，11D.28，22，10
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】現在給出三個條件：①a＝2；②B
；③c
b.試從中選出兩個條件，補充在下面的問題中，使其能夠確定△ABC，并以此為依據，求△ABC的面積.
在△ABC中，a、b、c分別是角A、B、C的對邊，且滿足
，求△ABC的面積（選出一種可行的方案解答，若選出多個方案分別解答，則按第一個解答記分）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在極坐標系中，直線l：
，P為直線l上一點，且點P在極軸上方
以OP為一邊作正三角形
逆時針方向
，且
面積為
．
求Q點的極坐標；
求外接圓的極坐標方程，并判斷直線l與外接圓的位置關系．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某地舉辦水果觀光采摘節，并推出配套旅游項目，統計了4月份100名游客購買水果的情況，得到如圖所示的頻率分布直方圖．
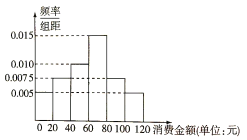
（1）若將消費金額不低于80元的游客稱為“水果達人”，現用分層抽樣的方法從樣本的“水果達人”中抽取5人，求這5人中消費金額不低于100元的人數；
（2）從（1）中的5人中抽取2人作為幸運客戶免費參加配套旅游項目，請列出所有的可能結果，并求這2人中至少有1人購買金額不低于100元的概率；
（3）為吸引顧客，該地特推出兩種促銷方案，
方案一：每滿80元可立減8元；
方案二：金額超過50元但又不超過80元的部分打9折，金額超過80元但又不超過100元的部分打8折，金額超過100元的部分打7折．
若水果的價格為11元／千克，某游客要購買10千克，應該選擇哪種方案.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
的方程為
，
是橢圓上的一點，且在第一象限內，過且斜率等于-1的直線與橢圓交于另一點
，點關于原點的對稱點為
．
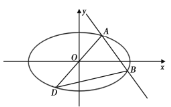
（1）證明：直線
的斜率為定值；
（2）求
面積的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在直角坐標系
中，曲線
的參數方程為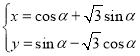
（
為參數），以坐標原點
為極點，
軸的正半軸為極軸，取相同長度單位建立極坐標系，直線
的極坐標方程為
.
（Ⅰ）求曲線和直線的直角坐標方程；
（Ⅱ）直線與
軸交點為
，經過點的直線與曲線交于
，
兩點，證明：
為定值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
