|
|
|
在△ABC中,a=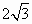  ,b= ,b=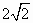 ,B=45°,則A等于 ,B=45°,則A等于
|
| [ ] |
A. |
30°
|
B. |
60°
|
C. |
60°或120°
|
D. |
30°或150°
|
|
|
練習冊系列答案
相關習題
科目:高中數學
來源:人民教育出版社(實驗修訂本) 高中數學
題型:
|
|
|
設等差數列{an}的前n項和為Sn,且a5+a13=34,S3=9.數列{bn}的前n項和為Tn,滿足Tn=1-bn.
(1)求數列{an}的通項公式;
(2)寫出一個正整數m,使得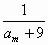 是數列{bn}的項; 是數列{bn}的項;
(3)設數列{cn}的通項公式為 ,問:是否存在正整數t和k(k≥3),使得c1,c2,ck成等差數列?若存在,請求出所有符合條件的有序整數對(t,k);若不存在,請說明理由. ,問:是否存在正整數t和k(k≥3),使得c1,c2,ck成等差數列?若存在,請求出所有符合條件的有序整數對(t,k);若不存在,請說明理由.
|
|
|
查看答案和解析>>
科目:高中數學
來源:人教B版(新課標) 必修2
題型:
|
|
|
若空間四邊形ABCD的兩條對角線AC,BD的長分別為4,6,過AB的中點E且平行BD,AC的截面四邊形的周長為________.
|
|
|
查看答案和解析>>
科目:高中數學
來源:人教B版(新課標) 必修5
題型:
|
|
|
在平面直角坐標系內,設M(x1,y1)、N(x2,y2)為不同的兩點,直線l的方程為ax+by+c=0,△1=ax1+by1+c,△2=ax2+by2+c.有四個命題:
①若△1△2>0,則點M、N一定在直線l的同側;
②若△1△2<0,則點M、N一定在直線l的兩側;
③若△1+△2=0,則點M、N一定在直線l的兩側;
④若 ,則點M到直線l的距離大于點N到直線l的距離. ,則點M到直線l的距離大于點N到直線l的距離.
上述命題中,全部真命題的序號是
|
| [ ] |
A. |
①②③
|
B. |
①②④
|
C. |
②③④
|
D. |
①②③④
|
|
|
查看答案和解析>>
科目:高中數學
來源:人教B版(新課標) 必修5
題型:
|
|
|
已知△ABC的周長為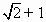 ,且sinA+sinB= ,且sinA+sinB=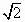 sinC. sinC.
(Ⅰ)求邊c的長;
(Ⅱ)若△ABC的面積為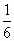 sinC,求角C的度數. sinC,求角C的度數.
|
|
|
查看答案和解析>>
科目:高中數學
來源:人教B版(新課標) 選修1-1
題型:
|
|
|
條件p∶-2<x<4,條件q∶(x+2)(x+a)<0;若p是q的充分而不必要條件,則a的取值范圍是
|
| [ ] |
A. |
(4,+∞)
|
B. |
(-∞,-4)
|
C. |
(-∞,-4]
|
D. |
[-4,+∞)
|
|
|
查看答案和解析>>
科目:高中數學
來源:人教B版(新課標) 選修4-5 不等式選講
題型:
|
|
|
設A(x1,y1),B(x2,y2)是平面直角坐標系上的兩點,定義點A到點B的曼哈頓距離L(A,B)=|x1-x2|+|y1-y2|.若點A(-1,1),B在y2=x上,則L(A,B)的最小值為________.
|
|
|
查看答案和解析>>
科目:高中數學
來源:蘇教版(新課標) 選修1-1
題型:
|
|
|
已知p: x∈R,x2+mx+1>0.若“ x∈R,x2+mx+1>0.若“ p”為真命題,則m的取值范圍是 p”為真命題,則m的取值范圍是
|
| [ ] |
A. |
(-2,2)
|
B. |
(-∞,-2)∪(2,+∞)
|
C. |
[-2,2]
|
D. |
(-∞,-2]∪[2,+∞)
|
|
|
查看答案和解析>>
