
在△ABC中,角A,B,C所對的邊長分別是a,b,c.
(1)若sin C + sin(B-A)= sin 2A,試判斷△ABC的形狀;
(2)若△ABC的面積S = 3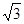 ,且c =
,且c =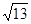 ,C =
,C =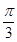 ,求a,b的值.
,求a,b的值.
(1)△ABC為直角三角形或等腰三角形(2)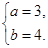
【解析】本試題主要是考查了解三角形的運用。
(1)根據三角形內角和定理,得到sinC=sin(A+B),代入已知等式,展開化簡合并,得sinBcosA=sinAcosA,最后討論當cosA=0時與當cosA≠0時,分別對△ABC的形狀的形狀加以判斷,可以得到結論
(2)結合三角形的面積公式和余弦定理得到結論。
解(1)由題意得 sin(B + A)+ sin(B-A)= sin 2A,
sin B cos A = sin A cos A,即 cos A(sin B-sin A)= 0,
cosA = 0 或 sin B = sin A. …… 3分
因A,B為三角形中的角,于是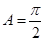 或B = A.
或B = A.
所以△ABC為直角三角形或等腰三角形. …… 5分
(2)因為△ABC的面積等于 3 ,所以
,所以
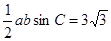 ,得 ab = 12.
,得 ab = 12.
由余弦定理及已知條件,得 a2 + b2-ab = 13.
聯立方程組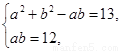 解得
解得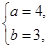 或
或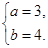 …………… 10分
…………… 10分


科目:高中數學 來源: 題型:
| 3 |
| 3 |
| A、a=c |
| B、b=c |
| C、2a=c |
| D、a2+b2=c2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 11 | 14 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| b |
| a |
| sinB |
| cosA |
| 2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com