
已知a1=2,點(an,an+1)在函數f(x)=x2+2x的圖象上,其中n=1,2,3,….
(1)求證:數列{lg(1+an)}是等比數列;
(2)設Tn=(1+a1)(1+a2)…(1+an),求Tn及數列{an}的通項;
(3)記![]() ,求數列{bn}的前n項和Sn,并證明
,求數列{bn}的前n項和Sn,并證明![]() .
.
|
(1)證明:由已知,得an+1=an2+2an, ∴an+1+1=(an+1)2.① ∵a1=2,∴an+1>1.將①式兩邊取對數,得 lg(1+an+1)=2lg(1+an),即 lg(1+a1)=lg(1+2)=lg3. ∴{lg(1+an)}是公比為2的等比數列. (2)解:由(1),知lg(1+an)=2n-1lg3=lg32n-1, ∴1+an=32n-1② ∴Tn=(1+a1)(1+a2)…(1+an)=320×321×322×…×32n-1=31+2+22+…+2n-1=32n-1. 由②式,得an=32n-1-1. (3)證明:∵an+1=an2+2an,∴an+1=an(an+2). ∴ ∴ 又 ∴ ∴ ∵an=32n-1-1,a1=2,an+1=32n-1, ∴ 又Tn=32n-1,∴ 思路分析:(1)主要根據已知條件找出相鄰兩項之間的關系,然后再證明;(2)要先求出數列an的通項公式;(3)在解題過程中恰當利用裂項相消可減少運算. |


科目:高中數學 來源:荊門市2008屆高三第一輪復習數列單元測試卷 題型:013
設數列{an}的前n項和為Sn,已知a1=5,且nSn+1=2n(n+1)+(n+1)Sn(n∈N*),則過點P(n,an)和Q(n+2,an+2)(n∈N*)的直線的一個方向向量的坐標可以是
A.(2,![]() )
)
B.(-1,-1)
C.(![]() ,-1)
,-1)
D.(![]() )
)
查看答案和解析>>
科目:高中數學 來源:全優設計選修數學-2-1蘇教版 蘇教版 題型:044
如圖α⊥β,α∩β=l,A∈α,B∈β,點A在直線l上的射影為A1,點B在l上的射影為B1,已知AB=2,AA1=1,BB1=![]() ,求:
,求:

(1)直線AB分別與平面α,β所成角的大小;
(2)二面角A1-AB-B1的大小.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年貴州省六盤水市高三10月月考文科數學(解析版) 題型:解答題
(本小題滿分12分)已知函數f(x)=x3+x2-2.
(1)設{an}是正數組成的數列,前n項和為Sn,其中a1=3.若點(an,an+12-2an+1)(n∈N*)在函數y=f′(x)的圖象上,求證:點(n,Sn)也在y=f′(x)的圖象上;
(2)求函數f(x)在區間(a-1,a)內的極值.
查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,α⊥β,α∩β=l,A∈α,B∈β,點A在直線l上的射影為A1,點B在直線l上的射影為B1,已知AB=2,AA1=1,BB1=
如圖,α⊥β,α∩β=l,A∈α,B∈β,點A在直線l上的射影為A1,點B在直線l上的射影為B1,已知AB=2,AA1=1,BB1=![]() ,求:
,求:
(Ⅰ)直線AB分別與平面α,β所成的角的大小;
(Ⅱ)二面角A1-AB-B1的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
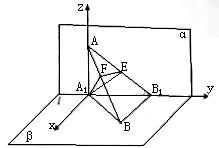
如圖,α⊥β,α∩β=l,A∈α,B∈β,點A在直線l上的射影為A1,點B在直線l上的射影為B1,已知AB=2,AA1=1,BB1=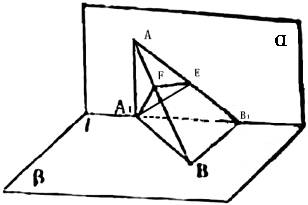 ,求:
,求:
(Ⅰ)直線AB分別與平面α,β所成的角的大小;
(Ⅱ)二面角A1-AB-B1的大小.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com