
20.(本小題滿分8分)如圖,AB是⊙O的直徑,PA⊥⊙O所在的平面,C是圓上一點,∠ABC = 30°,PA = AB.
 (1)求證:平面PAC⊥平面PBC;
(1)求證:平面PAC⊥平面PBC;
(2)求直線PC與平面ABC所成角的正切值;
(3)求二面角A—PB—C的正弦值.
解:(1)證明:∵AB是直徑 ∴∠ACB = 90°,即BC⊥AC
∴PA⊥BC
∴BC⊥平面PAC 又BC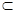 平面PBC
平面PBC
∴平面PBC⊥平面PAC
(2)∵PA⊥平面ABC
∴直線PC與平面ABC所成角即∠PCA
設AC = 1,∵∠ABC = 30°∴PA = AB = 2
∴tan∠PCA = = 2
(3) 在平面PAC中作AD⊥PC于D,在平面PAB中作AE⊥PB于連結DE
 ∵平面PAC⊥平面PBC,平面PAC∩平面PBC = PC,AD⊥PC
∵平面PAC⊥平面PBC,平面PAC∩平面PBC = PC,AD⊥PC
∴AD⊥平面PBC
∴AD⊥PB
又∵PB⊥AE ∴PB⊥面AED
∴PB⊥ED
∴∠DEA即為二面角A—PB—C的平面角
在直角三角形PAC中和直角三角形PAB中,
分別由等面積方法求得
AD = AE =
∴在直角三角形ADE中可求得:sin∠DEA =
即二面角A—PB—C的正弦值為.
【解析】略


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源:2012-2013年浙江臺州六校高二上期中聯考理科數學試卷(解析版) 題型:解答題
(本小題滿分8分)如圖四邊形 為梯形,
為梯形, ,
, ,求圖中陰影部分繞
,求圖中陰影部分繞 旋轉一周所形成的幾何體的表面積和體積。
旋轉一周所形成的幾何體的表面積和體積。

查看答案和解析>>
科目:高中數學 來源:2010年湖南省高二下學期學業水平第二次模擬考試數學試題 題型:解答題
(本小題滿分8分)
如圖,正方體 的棱長是2,
的棱長是2,
(1)求正方體 的外接球的表面積;
的外接球的表面積;
(2)求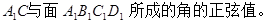

查看答案和解析>>
科目:高中數學 來源:2010年湖南省高二下學期學業水平第二次模擬考試數學試題 題型:解答題
(本小題滿分8分)如圖,等腰直角三角形ABC,AB= ,點E是斜邊AB上的動點,過E點做矩形EFCG,設矩形EFCG面積為S,矩形一邊EF長為
,點E是斜邊AB上的動點,過E點做矩形EFCG,設矩形EFCG面積為S,矩形一邊EF長為 ,
,
(1)將S表示為 的函數,并指出函數的定義域;
的函數,并指出函數的定義域;
(2)當 為何值時,矩形面積最大。(寫出過程)
為何值時,矩形面積最大。(寫出過程)

查看答案和解析>>
科目:高中數學 來源:2010年海南中學高一下學期期末測試數學 題型:解答題
(本小題滿分8分)
如圖,AB是⊙O的直徑,C為圓上一點,AB=2,AC=1,P為⊙O所在平面外一點,且PA垂直于⊙O所在平面,PB與⊙O所在平面成角 .求點A到平面PBC的距離.
.求點A到平面PBC的距離.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com