
【題目】已知函數![]() 在
在![]() 處取得極值A,函數
處取得極值A,函數![]() ,其中
,其中![]() …是自然對數的底數.
…是自然對數的底數.
(1)求m的值,并判斷A是![]() 的最大值還是最小值;
的最大值還是最小值;
(2)求![]() 的單調區間;
的單調區間;
(3)證明:對于任意正整數n,不等式![]() 成立.
成立.
【答案】(1)![]() ;
;![]() 是最小值;(2)單調遞減區間是
是最小值;(2)單調遞減區間是![]() ,單調遞增區間是
,單調遞增區間是![]() ;(3)證明過程見詳解.
;(3)證明過程見詳解.
【解析】
(1)先對函數求導,根據題意,得到![]() ,求出
,求出![]() ,研究函數單調性,即可判斷出結果;
,研究函數單調性,即可判斷出結果;
(2)對函數![]() 求導,得到
求導,得到![]() ,令
,令![]() ,對其求導,研究其單調性,即可判斷函數
,對其求導,研究其單調性,即可判斷函數![]() 的單調性;
的單調性;
(3)先由(1)得![]() 時,
時,![]() 恒成立,令
恒成立,令![]() ,則
,則![]() ,進而求和,即可得出結果.
,進而求和,即可得出結果.
(1)因為![]() ,
,![]() ,所以
,所以![]() ,
,
又![]() 在
在![]() 處取得極值
處取得極值![]() ,
,
則![]() ,即
,即![]() ;所以
;所以![]() ,
,
由![]() 得
得![]() ;由
;由![]() 得
得![]() ,
,
所以函數![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,
上單調遞增,
因此![]() 在
在![]() 處取得最小值,即
處取得最小值,即![]() 是最小值;
是最小值;
(2)由(1)得![]() ,
,
所以![]() ,
,
令![]() ,則
,則![]() ,
,
因為![]() ,所以
,所以![]() 恒成立,
恒成立,
因此![]() 在
在![]() 上單調遞增;又
上單調遞增;又![]() ,
,
所以,當![]() 時,
時,![]() ,即
,即![]() ;
;
當![]() 時,
時,![]() ,即
,即![]() ;
;
所以函數![]() 的單調遞減區間是
的單調遞減區間是![]() ,單調遞增區間是
,單調遞增區間是![]() ;
;
(3)由(1)知,![]() ,
,
所以![]() ,當
,當![]() 時,
時,![]() 恒成立;
恒成立;
令![]() ,則
,則![]() ,
,
因此![]()
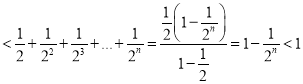 ,
,
即![]() ,
,
因此![]() .
.


 中考解讀考點精練系列答案
中考解讀考點精練系列答案科目:高中數學 來源: 題型:
【題目】在平行四邊形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是EA的中點(如圖1),將
是EA的中點(如圖1),將![]() 沿CD折起到圖2中
沿CD折起到圖2中![]() 的位置,得到四棱錐是
的位置,得到四棱錐是![]() .
.
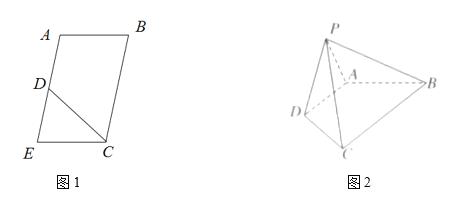
(1)求證:![]() 平面PDA;
平面PDA;
(2)若PD與平面ABCD所成的角為![]() .且
.且![]() 為銳角三角形,求平面PAD和平面PBC所成銳二面角的余弦值.
為銳角三角形,求平面PAD和平面PBC所成銳二面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】由團中央學校部、全國學聯秘書處、中國青年報社共同舉辦的2018年度全國“最美中學生”尋訪活動結果出爐啦,此項活動于2018年6月啟動,面向全國中學在校學生,通過投票方式尋訪一批在熱愛祖國、勤奮學習、熱心助人、見義勇為等方面表現突出、自覺樹立和踐行社會主義核心價值觀的“最美中學生”.現隨機抽取了30名學生的票數,繪成如圖所示的莖葉圖,若規定票數在65票以上(包括65票)定義為風華組.票數在65票以下(不包括65票)的學生定義為青春組.
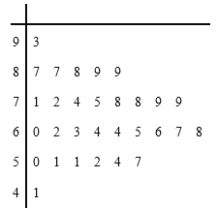
(1)如果用分層抽樣的方法從青春組和風華組中抽取5人,再從這5人中隨機抽取2人,那么至少有1人在青春組的概率是多少?
(2)用樣本估計總體,把頻率作為概率,若從該地區所有的中學(人數很多)中隨機選取4人,用![]() 表示所選4人中青春組的人數,試寫出
表示所選4人中青春組的人數,試寫出![]() 的分布列,并求出
的分布列,并求出![]() 的數學期望.
的數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】過拋物線![]() 上點
上點![]() 作三條斜率分別為
作三條斜率分別為![]() ,
,![]() ,
,![]() 的直線
的直線![]() ,
,![]() ,
,![]() ,與拋物線分別交于不同于
,與拋物線分別交于不同于![]() 的點
的點![]() .若
.若![]() ,
,![]() ,則以下結論正確的是( )
,則以下結論正確的是( )
A.直線![]() 過定點B.直線
過定點B.直線![]() 斜率一定
斜率一定
C.直線![]() 斜率一定D.直線
斜率一定D.直線![]() 斜率一定
斜率一定
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某汽車品牌為了了解客戶對于其旗下的五種型號汽車的滿意情況,隨機抽取了一些客戶進行回訪,調查結果如下表:
汽車型號 | I | II | III | IV | V |
回訪客戶(人數) | 250 | 100 | 200 | 700 | 350 |
滿意率 | 0.5 | 0.3 | 0.6 | 0.3 | 0.2 |
滿意率是指:某種型號汽車的回訪客戶中,滿意人數與總人數的比值.
假設客戶是否滿意互相獨立,且每種型號汽車客戶對于此型號汽車滿意的概率與表格中該型號汽車的滿意率相等.
(1)從所有的回訪客戶中隨機抽取1人,求這個客戶滿意的概率;
(2)從I型號和V型號汽車的所有客戶中各隨機抽取1人,設其中滿意的人數為![]() ,求
,求![]() 的分布列和期望;
的分布列和期望;
(3)用 “![]() ”, “
”, “![]() ”, “
”, “![]() ”, “
”, “![]() ”, “
”, “![]() ”分別表示I, II, III, IV, V型號汽車讓客戶滿意, “
”分別表示I, II, III, IV, V型號汽車讓客戶滿意, “![]() ”, “
”, “![]() ”, “
”, “![]() ”, “
”, “![]() ”, “
”, “![]() ” 分別表示I, II, III, IV, V型號汽車讓客戶不滿意.寫出方差
” 分別表示I, II, III, IV, V型號汽車讓客戶不滿意.寫出方差![]() 的大小關系.
的大小關系.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com