
【題目】在平行四邊形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是EA的中點(如圖1),將
是EA的中點(如圖1),將![]() 沿CD折起到圖2中
沿CD折起到圖2中![]() 的位置,得到四棱錐是
的位置,得到四棱錐是![]() .
.
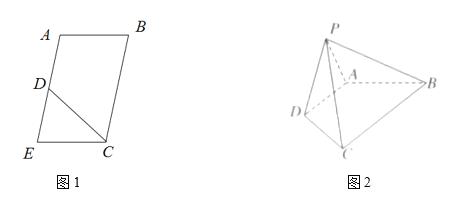
(1)求證:![]() 平面PDA;
平面PDA;
(2)若PD與平面ABCD所成的角為![]() .且
.且![]() 為銳角三角形,求平面PAD和平面PBC所成銳二面角的余弦值.
為銳角三角形,求平面PAD和平面PBC所成銳二面角的余弦值.
【答案】(1)證明見解析; (2)![]()
【解析】
(1)證明![]() ,
,![]() ,即可證明線面垂直;
,即可證明線面垂直;
(2)由線面角求得![]() ,以
,以![]() 中點
中點![]() 為坐標原點建立直角坐標系,由向量法求得二面角的余弦值.
為坐標原點建立直角坐標系,由向量法求得二面角的余弦值.
(1)將![]() 沿CD折起過程中,
沿CD折起過程中,![]() 平面PDA成立.證明如下:
平面PDA成立.證明如下:
![]() 是EA的中點,
是EA的中點,![]() ,
,![]() ,
,
在![]() 中,由余弦定理得,
中,由余弦定理得,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 為等腰直角三角形且
為等腰直角三角形且![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() 平面PDA.
平面PDA.
(2)由(1)知![]() 平面PDA,
平面PDA,![]() 平面ABCD,
平面ABCD,
![]() 平面
平面![]() 平面ABCD,
平面ABCD,
![]() 為銳角三角形,
為銳角三角形,
![]() 在平面ABCD內的射影必在棱AD上,記為O,連接PO,
在平面ABCD內的射影必在棱AD上,記為O,連接PO,![]() 平面ABCD,
平面ABCD,
則![]() 是PD與平面ABCD所成的角,
是PD與平面ABCD所成的角,
![]() ,
,
![]() ,
,
![]() 為等邊三角形,O為AD的中點,
為等邊三角形,O為AD的中點,
故以O為坐標原點,過點O且與CD平行的直線為x軸,
DA所在直線為y軸,OP所在直線為z軸建立如圖所示的空間直角坐標系,

設x軸與BC交于點M,
![]() ,
,![]()
易知![]()
![]() ,
,
則![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() 平面PDA,
平面PDA,
![]() 可取平面PDA的一個法向量
可取平面PDA的一個法向量![]() ,
,
設平面PBC的法向量![]() ,
,
則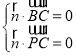 ,即
,即 ,
,
令![]() ,則
,則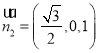 為平面PBC的一個法向量,
為平面PBC的一個法向量,
設平面PAD和平面PBC所成的角為![]() ,
,
由圖易知![]() 為銳角,
為銳角,
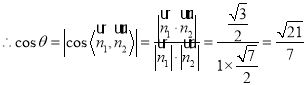 .
.
![]() 平面PAD和平面PBC所成角的余弦值為
平面PAD和平面PBC所成角的余弦值為![]() .
.


 黃岡天天練口算題卡系列答案
黃岡天天練口算題卡系列答案科目:高中數學 來源: 題型:
【題目】為了美化環境,某公園欲將一塊空地規劃建成休閑草坪,休閑草坪的形狀為如圖所示的四邊形ABCD.其中AB=3百米,AD=![]() 百米,且△BCD是以D為直角頂點的等腰直角三角形.擬修建兩條小路AC,BD(路的寬度忽略不計),設∠BAD=
百米,且△BCD是以D為直角頂點的等腰直角三角形.擬修建兩條小路AC,BD(路的寬度忽略不計),設∠BAD=![]() ,
,![]() (
(![]() ,
,![]() ).
).

(1)當cos![]() =
=![]() 時,求小路AC的長度;
時,求小路AC的長度;
(2)當草坪ABCD的面積最大時,求此時小路BD的長度.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知焦點在x軸的橢圓C:![]() 離心率e=
離心率e=![]() ,A是左頂點,E(2,0)
,A是左頂點,E(2,0)
(1)求橢圓C的標準方程:
(2)若斜率不為0的直線l過點E,且與橢圓C相交于點P,Q兩點,求三角形APQ面積的最大值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2018年11月21日,意大利奢侈品牌“![]() ﹠
﹠![]() ”在廣告中涉嫌辱華,中國明星紛紛站出來抵制該品牌,隨后京東、天貓、唯品會等中國電商平臺全線下架了該品牌商品,當天有大量網友關注此事件,某網上論壇從關注此事件跟帖中,隨機抽取了100名網友進行調查統計,先分別統計他們在跟帖中的留言條數,再把網友人數按留言條數分成6組:
”在廣告中涉嫌辱華,中國明星紛紛站出來抵制該品牌,隨后京東、天貓、唯品會等中國電商平臺全線下架了該品牌商品,當天有大量網友關注此事件,某網上論壇從關注此事件跟帖中,隨機抽取了100名網友進行調查統計,先分別統計他們在跟帖中的留言條數,再把網友人數按留言條數分成6組:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得到如圖所示的頻率分布直方圖;
,得到如圖所示的頻率分布直方圖;

并將其中留言不低于40條的規定為“強烈關注”,否則為“一般關注”,對這100名網友進一步統計得到列聯表的部分數據如下表.
一般關注 | 強烈關注 | 合計 | |
男 | 45 | ||
女 | 10 | 55 | |
合計 | 100 |
(1)在答題卡上補全列聯表中數據;并判斷能否有95%的把握認為網友對此事件是否為“強烈關注”與性別有關?
(2)現已從“強烈關注”的網友中按性別分層抽樣選取了5人,再從這5人中選取2人,求這2人中至少有1名女性的概率.
參考公式及數據:![]() ,
,
| 0.05 | 0.010 |
| 3.841 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:
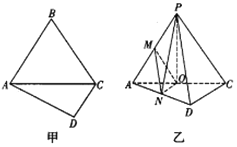
【題目】如圖所示甲,在四邊形ABCD中,![]() ,
,![]() ,
,![]() 是邊長為8的正三角形,把
是邊長為8的正三角形,把![]() 沿AC折起到
沿AC折起到![]() 的位置,使得平面
的位置,使得平面![]() 平面ACD,如圖所示乙所示,點O,M,N分別為棱AC,PA,AD的中點.
平面ACD,如圖所示乙所示,點O,M,N分別為棱AC,PA,AD的中點.
![]() 求證:
求證:![]() 平面PON;
平面PON;
![]() 求三棱錐
求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() ,圓
,圓![]() ,點
,點![]() 是圓上一動點,
是圓上一動點, ![]() 的垂直平分線與
的垂直平分線與![]() 交于點
交于點![]() .
.
(1)求點![]() 的軌跡方程;
的軌跡方程;
(2)設點![]() 的軌跡為曲線
的軌跡為曲線![]() ,過點
,過點![]() 且斜率不為0的直線
且斜率不為0的直線![]() 與
與![]() 交于
交于![]() 兩點,點
兩點,點![]() 關于
關于![]() 軸的對稱點為
軸的對稱點為![]() ,證明直線
,證明直線![]() 過定點,并求
過定點,并求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(Ⅰ)當a=1時,寫出![]() 的單調遞增區間(不需寫出推證過程);
的單調遞增區間(不需寫出推證過程);
(Ⅱ)當x>0時,若直線y=4與函數![]() 的圖像交于A,B兩點,記
的圖像交于A,B兩點,記![]() ,求
,求![]() 的最大值;
的最大值;
(Ⅲ)若關于x的方程![]() 在區間(1,2)上有兩個不同的實數根,求實數a的取值范圍.
在區間(1,2)上有兩個不同的實數根,求實數a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com