
【題目】已知函數![]() (a,
(a,![]() ).
).
(1)若![]() ,且
,且![]() 在
在![]() 內有且只有一個零點,求a的值;
內有且只有一個零點,求a的值;
(2)若![]() ,且
,且![]() 有三個不同零點,問是否存在實數a使得這三個零點成等差數列?若存在,求出a的值,若不存在,請說明理由;
有三個不同零點,問是否存在實數a使得這三個零點成等差數列?若存在,求出a的值,若不存在,請說明理由;
(3)若![]() ,
,![]() ,試討論是否存在
,試討論是否存在![]() ,使得
,使得![]() .
.
【答案】(1)![]() (2)存在;a的值為
(2)存在;a的值為![]() (3)答案不唯一,具體見解析
(3)答案不唯一,具體見解析
【解析】
(1)![]() ,
,![]() ,討論
,討論![]() 和
和![]() 兩種情況,分別計算函數的單調性,再根據零點個數得到參數.
兩種情況,分別計算函數的單調性,再根據零點個數得到參數.
(2)![]() ,根據題意
,根據題意![]() ,計算得到
,計算得到![]() ,
,![]() ,計算得到答案.
,計算得到答案.
(3)![]() ,
,![]() ,故必須
,故必須![]() 在
在![]() 上有解,解方程得到答案.
上有解,解方程得到答案.
(1)若![]() ,則
,則![]() ,
,![]() ,
,
若![]() ,則在
,則在![]() ,則
,則![]() ,則
,則![]() 在
在![]() 上單調遞增,
上單調遞增,
又![]() ,故
,故![]() 在
在![]() 上無零點,舍;
上無零點,舍;
若![]() ,令
,令![]() ,得
,得![]() ,
,![]() ,
,![]() ,
,
在![]() 上,
上,![]() ,
,![]() 在上單調遞減,
在上單調遞減,
在![]() 上,
上,![]() ,
,![]() 在上單調遞增,
在上單調遞增,
故![]() ,
,
若![]() ,則
,則![]() ,
,![]() 在
在![]() 上無零點,舍;
上無零點,舍;
若![]() ,則
,則![]() ,
,![]() 在
在![]() 上恰有一零點,此時
上恰有一零點,此時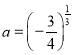 ;
;
若![]() ,則
,則![]() ,
,![]() ,
,![]() ,
,
則![]() 在
在![]() 和
和![]() 上有各有一個零點,舍;
上有各有一個零點,舍;
故a的值為![]() .
.
(2)因為![]() ,則
,則![]() ,若
,若![]() 有三個不同零點,且成等差數列,可設
有三個不同零點,且成等差數列,可設![]() ,
,
故![]() ,則
,則![]() ,故
,故![]() ,
,![]() ,
,![]() .
.
此時,![]() ,
,![]() ,故存在三個不同的零點.
,故存在三個不同的零點.
故符合題意的a的值為![]() .
.
(3)若![]() ,
,![]() ,
,![]() ,
,

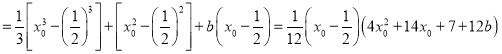
∴若存在![]() ,使得
,使得![]() ,
,
必須![]() 在
在![]() 上有解.
上有解.
![]() ,
,![]()
方程的兩根為:![]() ,
,![]() ,
,
![]() 只能是
只能是![]() ,
,
依題意![]() ,即
,即![]() ,
,![]()
即![]() ,
,
又由![]() ,得
,得![]() ,故欲使滿足題意的
,故欲使滿足題意的![]() 存在,則
存在,則![]() ,
,
∴當![]() 時,存在唯一的
時,存在唯一的![]() 滿足
滿足![]() ,
,
當![]() 時,不存在
時,不存在![]() 使
使![]() .
.


 小學課時特訓系列答案
小學課時特訓系列答案科目:高中數學 來源: 題型:
【題目】某工廠共有50位工人組裝某種零件.下面的散點圖反映了工人們組裝每個零件所用的工時(單位:分鐘)與人數的分布情況.由散點圖可得,這50位工人組裝每個零件所用工時的中位數為___________.若將500個要組裝的零件分給每個工人,讓他們同時開始組裝,則至少要過_________分鐘后,所有工人都完成組裝任務.(本題第一空2分,第二空3分)

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】汽車的“燃油效率”是指汽車每消耗1升汽油行駛的里程,下圖描述了甲、乙、丙三輛汽車在不同速度下的燃油效率情況. 下列敘述中正確的是( )

A. 消耗1升汽油,乙車最多可行駛5千米
B. 以相同速度行駛相同路程,三輛車中,甲車消耗汽油最多
C. 甲車以80千米/小時的速度行駛1小時,消耗10升汽油
D. 某城市機動車最高限速80千米/小時. 相同條件下,在該市用丙車比用乙車更省油
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設拋物線![]() 的焦點為
的焦點為![]() ,直線
,直線![]() 與拋物線交于
與拋物線交于![]() 兩點.
兩點.
(1)若![]() 過點
過點![]() ,且
,且![]() ,求
,求![]() 的斜率;
的斜率;
(2)若![]() ,且
,且![]() 的斜率為
的斜率為![]() ,當
,當![]() 時,求
時,求![]() 在
在![]() 軸上的截距的取值范圍(用
軸上的截距的取值范圍(用![]() 表示),并證明
表示),并證明![]() 的平分線始終與
的平分線始終與![]() 軸平行.
軸平行.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】足球比賽中,一隊在本方罰球區內犯規,會被判罰點球,點球是進攻方非常有效的得分手段.研究機構對某位足球隊員的1000次點球訓練進行了統計分析,以幫助球員提高點球的命中率.如圖,將球門框內的區域分成9個區域(區域代碼為1—9,球門框外的區域記做區域0),統計球員射點球時射中10個區域次數和進球次數(即使射中球門框內,也可能被守門員撲出),得到如下的兩個頻率分布條形圖:



(其中射中率![]() ,得分率
,得分率![]() )
)
(1)根據上述頻率分布條形圖,求射中球門框內時,各區域進球數的平均數(結果保留兩位小數)和中位數;
(2)以該隊員這1000次點球練習的進球頻率作為他在比賽中射點球時進球的概率,設他在三次射點球時進球數為![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國古代有輝煌的數學研究成果,其中《周髀算經》,《九章算術》,《海島算經》,《孫子算經》,《緝古算經》均有著十分豐富的內容,是了解我國古代數學的重要文獻,某中學計劃將這![]() 本專著作為高中階段“數學文化”樣本課程選修內容,要求每學年至少選一科,三學年必須將
本專著作為高中階段“數學文化”樣本課程選修內容,要求每學年至少選一科,三學年必須將![]() 門選完,則小南同學的不同選修方式有______種.
門選完,則小南同學的不同選修方式有______種.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com