【答案】
分析:由圖象知f(-1)=f(0)=f(2)=0,解出 b、c、d的值,由x
1和x
2是f
′ (x)=0的根,使用根與系數的關系得到x
1+x
2=

,x
1•x
2=-

,則由x
12+x
22 =(x
1+x
2)
2-2x
1•x
2 代入可求得結果.
解答:解:∵f(x)=x
3+bx
2+cx+d,由圖象知,-1+b-c+d=0,0+0+0+d=0,
8+4b+2c+d=0,∴d=0,b=-1,c=-2
∴f
′ (x)=3x
2+2bx+c=3x
2-2x-2. 由題意有 x
1 和 x
2 是函數f(x)的極值,
故有 x
1 和 x
2 是 f
′ (x)=0的根,∴x
1+x
2=

,x
1•x
2=-

.
則x
12+x
22 =(x
1+x
2)
2-2x
1•x
2=

+

=
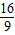
,
故選C.
點評:本題考查一元二次方程根的分布,根與系數的關系,函數在某點取的極值的條件,以及求函數的導數.



 x2
x2

 ,x1•x2=-
,x1•x2=- ,則由x12+x22 =(x1+x2)2-2x1•x2 代入可求得結果.
,則由x12+x22 =(x1+x2)2-2x1•x2 代入可求得結果. ,x1•x2=-
,x1•x2=- .
. +
+ =
=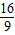 ,
,
