
【題目】已知圓![]() 與拋物線
與拋物線![]() 有一條斜率為1的公共切線
有一條斜率為1的公共切線![]() .
.
(1)求![]() .
.
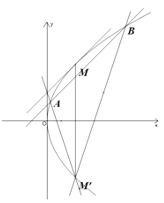
(2)設![]() 與拋物線切于點
與拋物線切于點![]() ,作點
,作點![]() 關于
關于![]() 軸的對稱點
軸的對稱點![]() ,在區域
,在區域![]() 內過
內過![]() 作兩條關于直線
作兩條關于直線![]() 對稱的拋物線的弦
對稱的拋物線的弦![]() ,
,![]() .連接
.連接![]() .
.
①求證:![]() ;
;
②設![]() 面積為
面積為![]() ,求
,求![]() 的最大值.
的最大值.
【答案】(1)![]() ,(2)①證明見解析,②
,(2)①證明見解析,②![]()
【解析】
(1)設切線為![]() ,其與圓相切,列方程可得可得
,其與圓相切,列方程可得可得![]() 的值,又與拋物線相切,與拋物線聯立,
的值,又與拋物線相切,與拋物線聯立,![]() ,結合
,結合![]() ,可求出
,可求出![]() 的值;
的值;
(2)①由(1)可得切點為![]() ,故
,故![]() ,設直線
,設直線![]() 方程為
方程為![]() ,點
,點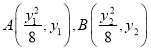 ,代入點的坐標可得
,代入點的坐標可得![]() 利用
利用![]() 與
與![]() 關于
關于![]() 對稱得到
對稱得到![]() ,聯立
,聯立![]() 與拋物線方程,結合韋達定理,可得
與拋物線方程,結合韋達定理,可得![]() ,即可證明
,即可證明![]() ;②求出
;②求出![]() 以及
以及![]() 到
到![]() 的距離,表示出
的距離,表示出![]() ,利用導數求其最值即可.
,利用導數求其最值即可.
(1)設切線為![]() .
.
∵直線與圓相切
∴![]() ,
,
解得![]() 或
或![]() ,
,
聯立![]() ,
,
得![]() ,
,
由![]() ,得
,得![]() .
.
結合![]() 可知:
可知:![]() ,
,![]() ;
;
(2)①由上述方程知直線與拋物線的切點為![]() ,故
,故![]() ,
,
設直線![]() 方程為
方程為![]() ,點
,點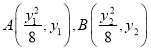
∴![]() ①
①
∵![]() 與
與![]() 關于
關于![]() 對稱
對稱
∴![]()
即:![]() ②
②
聯立![]() 與拋物線方程,
與拋物線方程,
![]() ,化簡整理得:
,化簡整理得:![]()
![]()
∴![]() ,
,![]() ,
,![]() ,
,
代入②式整理得![]() ,
,
∴ ![]() ;
;

②由①知,![]() 方程為
方程為![]() ,
,
結合條件及![]() 可知
可知![]() ,
,
又![]()
![]() 到
到![]() 的距離
的距離![]()
∴![]() .
.
考慮![]() 其中
其中![]() ,
,
![]() ,
,
當![]() 時,
時,![]() ,
,
此時![]() 的最大值為:
的最大值為:![]()


科目:高中數學 來源: 題型:
【題目】在直角坐標系中,以原點為極點,![]() 軸的正半軸為極軸,以相同的長度單位建立極坐標系,已知直線
軸的正半軸為極軸,以相同的長度單位建立極坐標系,已知直線![]() 的極坐標方程為
的極坐標方程為![]() ,曲線
,曲線![]() 的極坐標方程為
的極坐標方程為![]() ,
,![]()
(l)設![]() 為參數,若
為參數,若![]() ,求直線
,求直線![]() 的參數方程;
的參數方程;
(2)已知直線![]() 與曲線
與曲線![]() 交于
交于![]() ,
,![]() 設
設![]() ,且
,且![]() ,求實數
,求實數![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1,在矩形ABCD中,AB=4,AD=2,E是CD的中點,將△ADE沿AE折起,得到如圖2所示的四棱錐D1—ABCE,其中平面D1AE⊥平面ABCE.
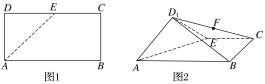
(1)證明:BE⊥平面D1AE;
(2)設F為CD1的中點,在線段AB上是否存在一點M,使得MF∥平面D1AE,若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖①,有一個長方體形狀的敞口玻璃容器,底面是邊長為20cm的正方形,高為30cm,內有20cm深的溶液.現將此容器傾斜一定角度![]() (圖②),且傾斜時底面的一條棱始終在桌面上(圖①、②均為容器的縱截面).
(圖②),且傾斜時底面的一條棱始終在桌面上(圖①、②均為容器的縱截面).
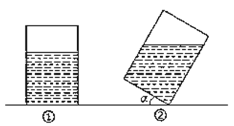
(1)要使傾斜后容器內的溶液不會溢出,角![]() 的最大值是多少?
的最大值是多少?
(2)現需要倒出不少于![]() 的溶液,當
的溶液,當![]() 時,能實現要求嗎?請說明理由.
時,能實現要求嗎?請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】公元263年左右,我國古代數學家劉徽用圓內接正多邊形的面積去逼近圓的面積求圓周率![]() ,他從單位圓內接正六邊形算起,令邊數一倍一倍地增加,即12,24,48,…,192,…,逐個算出正六邊形,正十二邊形,正二十四邊形,…,正一百九十二邊形,…的面積,這些數值逐步地逼近圓面積,劉徽算到了正一百九十二邊形,這時候
,他從單位圓內接正六邊形算起,令邊數一倍一倍地增加,即12,24,48,…,192,…,逐個算出正六邊形,正十二邊形,正二十四邊形,…,正一百九十二邊形,…的面積,這些數值逐步地逼近圓面積,劉徽算到了正一百九十二邊形,這時候![]() 的近似值是3.141024,劉徽稱這個方法為“割圓術”,并且把“割圓術”的特點概括為“割之彌細,所失彌少,割之又割,以至于不可割,則與圓周合體而無所失矣”.劉徽這種想法的可貴之處在于用已知的、可求的來逼近未知的、要求的,用有限來逼近無窮,這種思想極其重要,對后世產生了巨大影響.按照上面“割圓術”,用正二十四邊形來估算圓周率,則
的近似值是3.141024,劉徽稱這個方法為“割圓術”,并且把“割圓術”的特點概括為“割之彌細,所失彌少,割之又割,以至于不可割,則與圓周合體而無所失矣”.劉徽這種想法的可貴之處在于用已知的、可求的來逼近未知的、要求的,用有限來逼近無窮,這種思想極其重要,對后世產生了巨大影響.按照上面“割圓術”,用正二十四邊形來估算圓周率,則![]() 的近似值是( )(精確到
的近似值是( )(精確到![]() ).(參考數據
).(參考數據![]() )
)
A.3.14B.3.11C.3.10D.3.05
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,設橢圓![]() 兩頂點
兩頂點![]() ,短軸長為4,焦距為2,過點
,短軸長為4,焦距為2,過點![]() 的直線
的直線![]() 與橢圓交于
與橢圓交于![]() 兩點.設直線
兩點.設直線![]() 與直線
與直線![]() 交于點
交于點![]() .
.
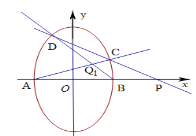
(1)求橢圓的方程;
(2)求線段![]() 中點
中點![]() 的軌跡方程;
的軌跡方程;
(3)求證:點![]() 的橫坐標為定值.
的橫坐標為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=lg ![]() ,f(1)=0,當x>0時,恒有f(x)
,f(1)=0,當x>0時,恒有f(x)![]() =lgx.
=lgx.
(1)若不等式f(x)≤lgt的解集為A,且A(0,4],求實數t的取值范圍;
(2)若方程f(x)=lg(8x+m)的解集為,求實數m的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com