
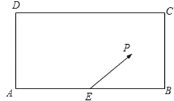
【題目】某校興趣小組在如圖所示的矩形區(qū)域![]() 內(nèi)舉行機器人攔截挑戰(zhàn)賽,在
內(nèi)舉行機器人攔截挑戰(zhàn)賽,在![]() 處按
處按![]() 方向釋放機器人甲,同時在
方向釋放機器人甲,同時在![]() 處按某方向釋放機器人乙,設(shè)機器人乙在
處按某方向釋放機器人乙,設(shè)機器人乙在![]() 處成功攔截機器人甲.若點
處成功攔截機器人甲.若點![]() 在矩形區(qū)域
在矩形區(qū)域![]() 內(nèi)(包含邊界),則挑戰(zhàn)成功,否則挑戰(zhàn)失敗.已知
內(nèi)(包含邊界),則挑戰(zhàn)成功,否則挑戰(zhàn)失敗.已知![]() 米,
米,![]() 為
為![]() 中點,機器人乙的速度是機器人甲的速度的2倍,比賽中兩機器人均按勻速直線運動方式行進,記
中點,機器人乙的速度是機器人甲的速度的2倍,比賽中兩機器人均按勻速直線運動方式行進,記![]() 與
與![]() 的夾角為
的夾角為![]() .
.
(1)若![]() ,
,![]() 足夠長,則如何設(shè)置機器人乙的釋放角度才能挑戰(zhàn)成功?(結(jié)果精確到
足夠長,則如何設(shè)置機器人乙的釋放角度才能挑戰(zhàn)成功?(結(jié)果精確到![]() );
);
(2)如何設(shè)計矩形區(qū)域![]() 的寬
的寬![]() 的長度,才能確保無論
的長度,才能確保無論![]() 的值為多少,總可以通過設(shè)置機器人乙的釋放角度使機器人乙在矩形區(qū)域
的值為多少,總可以通過設(shè)置機器人乙的釋放角度使機器人乙在矩形區(qū)域![]() 內(nèi)成功攔截機器人甲?
內(nèi)成功攔截機器人甲?
【答案】(1)按照與![]() 夾角為
夾角為![]() 的向量
的向量![]() 方向釋放機器人乙;(2)
方向釋放機器人乙;(2)![]() 米
米
【解析】
(1)利用正弦定理,即可求解;
(2)以![]() 所在直線為
所在直線為![]() 軸,
軸,![]() 中垂線為
中垂線為![]() 軸,建平面直角坐標系,求出
軸,建平面直角坐標系,求出![]() 的軌跡方程,即可得出結(jié)論.
的軌跡方程,即可得出結(jié)論.
(1)![]() 中,
中,![]() ,
,![]() ,
,
由正弦定理,得:![]() ,
,
所以![]() ,所以
,所以![]() .
.
所以應(yīng)在矩形區(qū)域![]() 內(nèi),按照與
內(nèi),按照與![]() 夾角為
夾角為![]()
的向量![]() 方向釋放機器人乙,才能挑戰(zhàn)成功.
方向釋放機器人乙,才能挑戰(zhàn)成功.
(2)以![]() 所在直線為
所在直線為![]() 軸,
軸,![]() 中垂線為
中垂線為![]() 軸,
軸,
建平面直角坐標系,設(shè)![]() 由題意,
由題意,
知![]() ,所以
,所以![]() ,
,
所以![]()
即點![]() 的軌跡是以
的軌跡是以![]() 為圓心,6為半
為圓心,6為半
徑的上半圓在矩形區(qū)域![]() 內(nèi)的部分.
內(nèi)的部分.
所以當![]() 米時,能確保無論
米時,能確保無論![]() 的值為多少,
的值為多少,
總可以通過設(shè)置機器人乙的釋放角度使機器人
乙在矩形區(qū)域![]() 內(nèi)成功攔截機器人甲.
內(nèi)成功攔截機器人甲.


科目:高中數(shù)學 來源: 題型:
【題目】設(shè)數(shù)列![]() 為首項是4,公差為1的等差數(shù)列,
為首項是4,公差為1的等差數(shù)列,![]() 為數(shù)列
為數(shù)列![]() 的前
的前![]() 項和,且
項和,且![]() 。
。
(1)求數(shù)列![]() 及
及![]() 的通項公式
的通項公式![]() 和
和![]() ;
;
(2)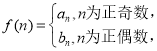 問是否存在
問是否存在![]() 使
使![]() 成立?若存在,求出
成立?若存在,求出![]() ,若不存在,說明理由;
,若不存在,說明理由;
(3)對任意的正數(shù)![]() ,不等式
,不等式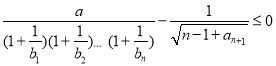 恒成立,求正數(shù)
恒成立,求正數(shù)![]() 的取值范圍。
的取值范圍。
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】對于函數(shù)y=f(x),x∈D,若存在閉區(qū)間[a,b]![]() 和常數(shù)C,使得對任意x∈[a,b]都有f(x)=C,稱f(x)為“橋函數(shù)”.
和常數(shù)C,使得對任意x∈[a,b]都有f(x)=C,稱f(x)為“橋函數(shù)”.
(1)作出函數(shù)![]() 的圖象,并說明f(x)是否為“橋函數(shù)”?(不必證明)
的圖象,并說明f(x)是否為“橋函數(shù)”?(不必證明)
(2)設(shè)f(x)定義域為R,判斷“f(x)為奇函數(shù)”是“![]() 為’橋函數(shù)’”的什么條件?給出你的結(jié)論并說明理由;
為’橋函數(shù)’”的什么條件?給出你的結(jié)論并說明理由;
(3)若函數(shù)![]() 是“橋函數(shù)”,求常數(shù)m、n的值.
是“橋函數(shù)”,求常數(shù)m、n的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
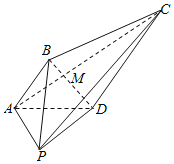
【題目】在四棱錐P–ABCD中,![]() ,
,![]() .
.
(1)設(shè)AC與BD相交于點M,![]() ,且
,且![]() 平面PCD,求實數(shù)m的值;
平面PCD,求實數(shù)m的值;
(2)若![]() ,
,![]() ,
,![]() ,且
,且![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】若函數(shù)![]() 與
與![]() 在給定的區(qū)間上滿足
在給定的區(qū)間上滿足![]() 恒成立,則稱這兩個函數(shù)在該區(qū)間上“和諧”。
恒成立,則稱這兩個函數(shù)在該區(qū)間上“和諧”。
(1)若函數(shù)![]() 與
與![]() 在R上和諧,求實數(shù)a的取值范圍;
在R上和諧,求實數(shù)a的取值范圍;
(2)若函數(shù)![]() 與
與![]() 在
在![]() 上和諧,求實數(shù)a的取值范圍.
上和諧,求實數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】選修4—4:極坐標與參數(shù)方程
在平面直角坐標系![]() 中,將曲線
中,將曲線![]() (
(![]() 為參數(shù)) 上任意一點
為參數(shù)) 上任意一點![]() 經(jīng)過伸縮變換
經(jīng)過伸縮變換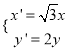 后得到曲線
后得到曲線![]() 的圖形.以坐標原點
的圖形.以坐標原點![]() 為極點,x軸的非負半軸為極軸,取相同的單位長度建立極坐標系,已知直線
為極點,x軸的非負半軸為極軸,取相同的單位長度建立極坐標系,已知直線![]() .
.
(Ⅰ)求曲線![]() 和直線
和直線![]() 的普通方程;
的普通方程;
(Ⅱ)點P為曲線![]() 上的任意一點,求點P到直線
上的任意一點,求點P到直線![]() 的距離的最大值及取得最大值時點P的坐標.
的距離的最大值及取得最大值時點P的坐標.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】“割圓術(shù)”是劉徽最突出的數(shù)學成就之一,他在《九章算術(shù)注》中提出割圓術(shù),并作為計算圓的周長,面積已經(jīng)圓周率的基礎(chǔ),劉徽把圓內(nèi)接正多邊形的面積一直算到了正3072邊形,并由此而求得了圓周率為3.1415和3.1416這兩個近似數(shù)值,這個結(jié)果是當時世界上圓周率計算的最精確數(shù)據(jù).如圖,當分割到圓內(nèi)接正六邊形時,某同學利用計算機隨機模擬法向圓內(nèi)隨機投擲點,計算得出該點落在正六邊形內(nèi)的頻率為0.8269,那么通過該實驗計算出來的圓周率近似值為(參考數(shù)據(jù):![]() )
)

A. 3.1419B. 3.1417C. 3.1415D. 3.1413
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() 的一個焦點為
的一個焦點為![]() ,離心率
,離心率![]() ,左,右頂點分別為A,B,經(jīng)過點F的直線與橢圓交于C,D兩點(與A,B不重合).
,左,右頂點分別為A,B,經(jīng)過點F的直線與橢圓交于C,D兩點(與A,B不重合).
(1)求橢圓M的方程;
(2)記![]() 與
與![]() 的面積分別為
的面積分別為![]() 和
和![]() ,求
,求![]() |的最大值.
|的最大值.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com