Question

如圖,PA⊥平面ABCD,四邊形ABCD是矩形,PA=AD=a,M、N分別是AB、PC的中點.

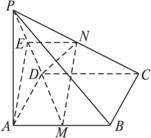
(1)求平面PCD與平面ABCD所成二面角的大小;

(2)求證:平面MND⊥平面PCD;

(3)當AB的長度變化時,求異面直線PC與AD所成角的取值范圍.

Answer 1

(1)解：PA⊥平面ABCD,CD⊥AD,

    ∴PD⊥CD.

    故∠PDA是平面PCD與平面ABCD所成二面角的平面角.

    在Rt△PAD中,PA⊥AD,PA=AD,

    ∴∠PDA=45°.

(2)證明:如圖所示,取PD中點E,連結AE、EN,由M、N分別是AB、PC的中點,

    ∴ENCDAB.

    ∴AMNE為平行四邊形.

    ∴MN∥AE.在等腰Rt△PAD中,AE是斜邊的中線,

    ∴AE⊥PD.

    又CD⊥PD,CD⊥AD,

    ∴CD⊥平面PAD.

    ∴CD⊥AE.

    又PD∩CD=D,

    ∴AE⊥平面PCD.

    ∴MN⊥平面PCD.

    ∴平面MND⊥平面PCD.

(3)解:∵AD∥BC,

    ∴∠PCB為異面直線PC、AD所成的角,由三垂線定理知PB⊥BC,

    設AB=x(x＞0),

    ∴tan∠PCB==＞1.

    又∠PCB為銳角,

    ∴∠PCB∈(,),

    即異面直線PC、AD所成角的范圍是(,).