
分析 (1)設ξ表示游戲終止時擲硬幣的次數,正面出現的次數為m,反面出現的次數為n,則$\left\{\begin{array}{l}{|m-n|=5}\\{m+n=ξ}\\{1≤ξ≤7}\end{array}\right.$.對m分類討論即可得出.
(2)假設A贏了B,5次終止,那么A贏了4次,B贏了1次. B的這一次只能發(fā)生在前三次中(前三中還不發(fā)生,A就贏了),也就是有三種情況,每種情況概率均為$(\frac{1}{2})^{5}$,且還有B贏A的情況,則最后概率為$(\frac{1}{2})^{5}×3×2$=$\frac{3}{16}$.
解答 解:(1)設ξ表示游戲終止時擲硬幣的次數,
正面出現的次數為m,反面出現的次數為n,則$\left\{\begin{array}{l}{|m-n|=5}\\{m+n=ξ}\\{1≤ξ≤7}\end{array}\right.$.
可得:當m=5,n=0或m=0,n=5時,ξ=5;
當m=6,n=1或m=1,n=6時,ξ=7.
所以ξ的所有可能取值為:5,7.
P(ξ≤7)=P(ξ=5)+P(ξ=7)=2$(\frac{1}{2})^{5}$+2${∁}_{5}^{1}×(\frac{1}{2})^{7}$=$\frac{9}{64}$.
(2)ξ表示“游戲已進行五次時同學A擁有的卡片數”,則ξ=0,1,2,3,4,7,8,9,10.
假設A贏了B,5次終止,那么A贏了4次,B贏了1次. B的這一次只能發(fā)生在前三次中(前三中還不發(fā)生,A就贏了),也就是有三種情況,每種情況概率均為$(\frac{1}{2})^{5}$,且還有B贏A的情況,則最后概率為$(\frac{1}{2})^{5}×3×2$=$\frac{3}{16}$.
點評 本題考查了二項分布列的概率與首項期望計算公式、古典概率計算公式,考查了推理能力與計算能力,屬于中檔題.


 浙大優(yōu)學小學年級銜接捷徑浙江大學出版社系列答案
浙大優(yōu)學小學年級銜接捷徑浙江大學出版社系列答案科目:高中數學 來源: 題型:選擇題
| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{\sqrt{10}}{5}$ | C. | $\frac{2\sqrt{5}}{5}$ | D. | $\frac{2\sqrt{10}}{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
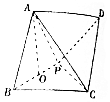 如圖,在四棱錐P-ABCD中,底面ABCD是菱形,且AB=$\sqrt{2}$,∠ABC=60°,點A在平面PBC上的射影為PB的中點O,PB⊥AC.
如圖,在四棱錐P-ABCD中,底面ABCD是菱形,且AB=$\sqrt{2}$,∠ABC=60°,點A在平面PBC上的射影為PB的中點O,PB⊥AC.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {-2,-1} | B. | {0,1} | C. | {-1,0,1} | D. | {0,1,2} |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com