
【題目】設(shè)函數(shù)![]() ,
, ![]() .
.
(1)求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)若函數(shù)![]() 在
在![]() 處取得極大值,求正實(shí)數(shù)
處取得極大值,求正實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
【答案】(1)見解析;(2)正實(shí)數(shù)![]() 的取值范圍為
的取值范圍為![]() 。
。
【解析】試題分析:(1)求出![]() ,分兩種情況討論,分別令
,分兩種情況討論,分別令![]() 求得
求得![]() 的范圍,可得函數(shù)
的范圍,可得函數(shù)![]() 增區(qū)間,
增區(qū)間, ![]() 求得
求得![]() 的范圍,可得函數(shù)
的范圍,可得函數(shù)![]() 的減區(qū)間;(2)討論
的減區(qū)間;(2)討論![]() 的取值范圍,分別利用導(dǎo)數(shù)研究函數(shù)的單調(diào)性,根據(jù)函數(shù)極值的定義,進(jìn)行驗(yàn)證即可得到結(jié)論.
的取值范圍,分別利用導(dǎo)數(shù)研究函數(shù)的單調(diào)性,根據(jù)函數(shù)極值的定義,進(jìn)行驗(yàn)證即可得到結(jié)論.
試題解析:(1)由![]() ,
,
所以![]() .
.
當(dāng)![]() 時(shí),
時(shí), ![]() ,函數(shù)
,函數(shù)![]() 在
在![]() 上單調(diào)遞增;
上單調(diào)遞增;
當(dāng)![]() 時(shí),
時(shí), ![]() ,函數(shù)
,函數(shù)![]() 單調(diào)遞增,
單調(diào)遞增, ![]() 時(shí),
時(shí), ![]() ,函數(shù)
,函數(shù)![]() 單調(diào)遞減.
單調(diào)遞減.
所以當(dāng)![]() 時(shí),
時(shí), ![]() 的單調(diào)增區(qū)間為
的單調(diào)增區(qū)間為![]() ;
;
當(dāng)![]() 時(shí),
時(shí), ![]() 的單調(diào)增區(qū)間為
的單調(diào)增區(qū)間為![]() ,單調(diào)減區(qū)間為
,單調(diào)減區(qū)間為![]() .
.
(2)∵![]() ,
,
∴![]() 且
且![]() .
.
由(1)知①當(dāng)![]() 時(shí),
時(shí), ![]() ,由(1)知
,由(1)知![]() 在
在![]() 內(nèi)單調(diào)遞增,可得當(dāng)
內(nèi)單調(diào)遞增,可得當(dāng)![]() 時(shí),
時(shí), ![]() ,當(dāng)
,當(dāng)![]() 時(shí),
時(shí), ![]() .
.
所以![]() 在
在![]() 內(nèi)單調(diào)遞減,在
內(nèi)單調(diào)遞減,在![]() 內(nèi)單調(diào)遞增,所以
內(nèi)單調(diào)遞增,所以![]() 在
在![]() 處取得極小值,不合題意.
處取得極小值,不合題意.
②當(dāng)![]() 時(shí),
時(shí), ![]() ,
, ![]() 在
在![]() 內(nèi)單調(diào)遞增,在
內(nèi)單調(diào)遞增,在![]() 內(nèi)單調(diào)遞減,所以當(dāng)
內(nèi)單調(diào)遞減,所以當(dāng)![]() 時(shí),
時(shí), ![]() ,
, ![]() 單調(diào)遞減,不合題意.
單調(diào)遞減,不合題意.
③當(dāng)![]() 時(shí),
時(shí), ![]() ,當(dāng)
,當(dāng)![]() 時(shí),
時(shí), ![]() ,
, ![]() 單調(diào)遞增,當(dāng)
單調(diào)遞增,當(dāng)![]() 時(shí),
時(shí), ![]() ,
, ![]() 單調(diào)遞減.
單調(diào)遞減.
所以![]() 在
在![]() 處取得極大值,符合題意.
處取得極大值,符合題意.
綜上可知,正實(shí)數(shù)![]() 的取值范圍為
的取值范圍為![]() .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】若執(zhí)行右側(cè)的程序框圖,當(dāng)輸入的x的值為4時(shí),輸出的y的值為2,則空白判斷框中的條件可能為( ) 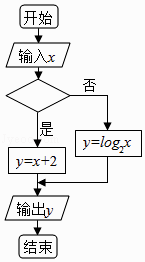
A.x>3
B.x>4
C.x≤4
D.x≤5
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某商場(chǎng)為吸引顧客消費(fèi)推出一項(xiàng)優(yōu)惠活動(dòng).活動(dòng)規(guī)則如下:消費(fèi)額每滿100元可轉(zhuǎn)動(dòng)如圖所示的轉(zhuǎn)盤一次,并獲得相應(yīng)金額的返券,假定指針等可能地停在任一位置.若指針停在A區(qū)域返券60元;停在B區(qū)域返券30元;停在C區(qū)域不返券.例如:消費(fèi)218元,可轉(zhuǎn)動(dòng)轉(zhuǎn)盤2次,所獲得的返券金額是兩次金額之和.

(1)若某位顧客消費(fèi)128元,求返券金額不低于30元的概率;
(2)若某位顧客恰好消費(fèi)280元,并按規(guī)則參與了活動(dòng),他獲得返券的金額記為![]() (元).求隨機(jī)變量
(元).求隨機(jī)變量![]() 的分布列和數(shù)學(xué)期望.
的分布列和數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】根據(jù)《中華人民共和國(guó)道路交通安全法》規(guī)定:“車輛駕駛員血液酒精溶度(單位mg/100ml)/在![]() ,屬于酒后駕駛;血液濃度不低于80,屬于醉酒駕駛。”2017年“中秋節(jié)”晚9點(diǎn)開始,濟(jì)南市交警隊(duì)在桿石橋交通崗前設(shè)點(diǎn),對(duì)過往的車輛進(jìn)行檢查,經(jīng)過4個(gè)小時(shí),共查處喝過酒的駕駛者60名,下圖是用酒精測(cè)試儀對(duì)這60名駕駛者血液中酒精溶度進(jìn)行檢測(cè)后所得結(jié)果畫出的頻率分布直方圖。
,屬于酒后駕駛;血液濃度不低于80,屬于醉酒駕駛。”2017年“中秋節(jié)”晚9點(diǎn)開始,濟(jì)南市交警隊(duì)在桿石橋交通崗前設(shè)點(diǎn),對(duì)過往的車輛進(jìn)行檢查,經(jīng)過4個(gè)小時(shí),共查處喝過酒的駕駛者60名,下圖是用酒精測(cè)試儀對(duì)這60名駕駛者血液中酒精溶度進(jìn)行檢測(cè)后所得結(jié)果畫出的頻率分布直方圖。
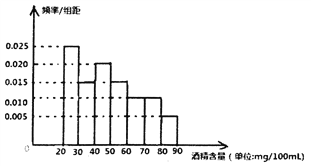
(1)求這60名駕駛者中屬于醉酒駕車的人數(shù)(圖中每組包括左端點(diǎn),不包括右端點(diǎn))
(2)若以各小組的中值為該組的估計(jì)值,頻率為概率的估計(jì)值,求這60名駕駛者血液的酒精濃度的平均值。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知數(shù)列![]() 各項(xiàng)均為正數(shù),
各項(xiàng)均為正數(shù), ![]() ,
, ![]() ,且
,且![]() 對(duì)任意
對(duì)任意![]() 恒成立,記
恒成立,記![]() 的前
的前![]() 項(xiàng)和為
項(xiàng)和為![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)證明:對(duì)任意正實(shí)數(shù)![]() ,
, ![]() 成等比數(shù)列;
成等比數(shù)列;
(3)是否存在正實(shí)數(shù)![]() ,使得數(shù)列
,使得數(shù)列![]() 為等比數(shù)列.若存在,求出此時(shí)
為等比數(shù)列.若存在,求出此時(shí)![]() 和
和![]() 的表達(dá)式;若不存在,說明理由.
的表達(dá)式;若不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知拋物線![]() :
: ![]() 的焦點(diǎn)為
的焦點(diǎn)為![]() ,過
,過![]() 的直線
的直線![]() 交拋物線
交拋物線![]() 于點(diǎn)
于點(diǎn)![]() ,當(dāng)直線
,當(dāng)直線![]() 的傾斜角是
的傾斜角是![]() 時(shí),
時(shí), ![]() 的中垂線交
的中垂線交![]() 軸于點(diǎn)
軸于點(diǎn)![]() .
.

(1)求![]() 的值;
的值;
(2)以![]() 為直徑的圓交
為直徑的圓交![]() 軸于點(diǎn)
軸于點(diǎn)![]() ,記劣弧
,記劣弧![]() 的長(zhǎng)度為
的長(zhǎng)度為![]() ,當(dāng)直線
,當(dāng)直線![]() 繞
繞![]() 點(diǎn)旋轉(zhuǎn)時(shí),求
點(diǎn)旋轉(zhuǎn)時(shí),求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在直角坐標(biāo)系![]() 中,以
中,以![]() 為極點(diǎn),
為極點(diǎn), ![]() 軸正半軸為極軸建立極坐標(biāo)系,曲線
軸正半軸為極軸建立極坐標(biāo)系,曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() ,
, ![]() 是曲線
是曲線![]() 與直線
與直線![]() :
: ![]() (
(![]() )的交點(diǎn)(異于原點(diǎn)
)的交點(diǎn)(異于原點(diǎn)![]() ).
).
(1)寫出![]() ,
, ![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)求過點(diǎn)![]() 和直線
和直線![]() 垂直的直線
垂直的直線![]() 的極坐標(biāo)方程.
的極坐標(biāo)方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)= ![]() -
-![]() ,g(x)=
,g(x)= ![]() .
.
(1)若![]() ,函數(shù)
,函數(shù)![]() 的圖像與函數(shù)
的圖像與函數(shù)![]() 的圖像相切,求
的圖像相切,求![]() 的值;
的值;
(2)若![]() ,
, ![]() ,函數(shù)
,函數(shù)![]() 滿足對(duì)任意
滿足對(duì)任意![]() (x1
(x1![]() x2),都有
x2),都有![]() 恒成立,求
恒成立,求![]() 的取值范圍;
的取值范圍;
(3)若![]() ,函數(shù)
,函數(shù)![]() =f(x)+ g(x),且G(
=f(x)+ g(x),且G(![]() )有兩個(gè)極值點(diǎn)x1,x2,其中x1
)有兩個(gè)極值點(diǎn)x1,x2,其中x1![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com