
【題目】已知函數(shù)f(x)=lnx,g(x)=0.5x2-bx, (b為常數(shù))。
(1)函數(shù)f(x)的圖象在點(1,f(1))處的切線與函數(shù)g(x)的圖象相切,求實數(shù)b的值;
(2)若函數(shù)h(x)=f(x)+g(x)在定義域上不單調(diào),求實數(shù)b的取值范圍;
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】試題分析:(1)求出函數(shù)的導函數(shù),從而可得![]() ,點斜式求得切線方程,根據(jù)判別式為零求出
,點斜式求得切線方程,根據(jù)判別式為零求出![]() 的值即可;(2)求出
的值即可;(2)求出![]() 的導數(shù),若函數(shù)在定義域內(nèi)不單調(diào),可知
的導數(shù),若函數(shù)在定義域內(nèi)不單調(diào),可知![]() 在
在![]() 上有解,結合二次函數(shù)的性質(zhì)得到關于
上有解,結合二次函數(shù)的性質(zhì)得到關于![]() 的不等式組,解出即可.
的不等式組,解出即可.
試題解析:(1)因為![]() ,所以
,所以![]() ,因此
,因此![]() ,
,
所以函數(shù)![]() 的圖象在點
的圖象在點![]() 處的切線方程為
處的切線方程為![]() ,
,
由 得
得![]() .
.
由![]() ,得
,得![]() .(還可以通過導數(shù)來求).
.(還可以通過導數(shù)來求).
(2)因為h(x)=f(x)+g(x)=lnx+0.5x2-bx(x>0) ,
所以![]()
若函數(shù)在定義域內(nèi)不單調(diào),則
可知![]() 在
在![]() 上有解,
上有解,
因為![]() ,設
,設![]() ,因為
,因為![]() ,
,
則只要 解得
解得![]() ,
,
所以的取值范圍是![]() .
.
【方法點晴】本題主要考查利用導數(shù)求曲線切線以及二次函數(shù)的性質(zhì),屬于難題.求曲線切線方程的一般步驟是:(1)求出![]() 在
在![]() 處的導數(shù),即
處的導數(shù),即![]() 在點
在點![]()
![]() 出的切線斜率(當曲線
出的切線斜率(當曲線![]() 在
在![]() 處的切線與
處的切線與![]() 軸平行時,在 處導數(shù)不存在,切線方程為
軸平行時,在 處導數(shù)不存在,切線方程為![]() );(2)由點斜式求得切線方程
);(2)由點斜式求得切線方程![]() .
.


 津橋教育計算小狀元系列答案
津橋教育計算小狀元系列答案科目:高中數(shù)學 來源: 題型:
【題目】設全集U=R,集合A={x|-1≤x<3},B={x|2x-4≥x-2}.
(1)求U(A∩B);
(2)若集合C={x|2x+a>0},滿足B∪C=C,求實數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】定義區(qū)間(a,b),[a,b),(a,b],[a,b]的長度均為![]() ,多個區(qū)間并集的長度為各區(qū)間長度之和,例如,(1,2)
,多個區(qū)間并集的長度為各區(qū)間長度之和,例如,(1,2) ![]() [3,5)的長度d=(2-1)+(5-3)=3. 用[x]表示不超過x的最大整數(shù),記{x}=x-[x],其中
[3,5)的長度d=(2-1)+(5-3)=3. 用[x]表示不超過x的最大整數(shù),記{x}=x-[x],其中![]() .設
.設![]() ,
, ![]() ,當
,當![]() 時,不等式
時,不等式![]() 解集區(qū)間的長度為
解集區(qū)間的長度為![]() ,則
,則![]() 的值為_______.
的值為_______.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知三棱錐A-BCD中,△ABC是等腰直角三角形,且AC⊥BC,BC=2,AD⊥平面BCD,AD=1.
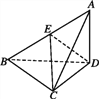
(1)求證:平面ABC⊥平面ACD;
(2)若E為AB中點,求點A到平面CED的距離.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() 的兩個焦點分別為
的兩個焦點分別為![]() ,離心率為
,離心率為![]() .設過點
.設過點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 相交于不同兩點
相交于不同兩點![]() ,
, ![]() 周長為
周長為![]() .
.
(Ⅰ)求橢圓C的標準方程;
(Ⅱ)已知點![]() ,證明:當直線
,證明:當直線![]() 變化時,總有TA與
變化時,總有TA與![]() 的斜率之和為定值.
的斜率之和為定值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
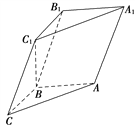
【題目】如圖,在三棱柱ABCA1B1C1中,已知AB⊥側面BB1C1C,AB=BC=1,BB1=2,∠BCC1=![]() .
.
(1)求證:C1B⊥平面ABC;
設![]() (0≤λ≤1),且平面AB1E與BB1E所成的銳二面角的大小為30°,
(0≤λ≤1),且平面AB1E與BB1E所成的銳二面角的大小為30°,
試求λ的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() ,且
,且![]() .
.
(1)判斷函數(shù)![]() 的奇偶性;
的奇偶性;
(2) 判斷函數(shù)![]() 在(1,+∞)上的單調(diào)性,并用定義證明你的結論;
在(1,+∞)上的單調(diào)性,并用定義證明你的結論;
(3)若![]() ,求實數(shù)a的取值范圍.
,求實數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】選修![]() :坐標系與參數(shù)方程
:坐標系與參數(shù)方程
已知曲線C的極坐標方程為ρ﹣4cosθ+3ρsin2θ=0,以極點為原點,極軸為x軸的正半軸建立平面直角坐標系,直線l過點M(1,0),傾斜角為![]() .
.
(Ⅰ)求曲線C的直角坐標方程與直線l的參數(shù)方程;
(Ⅱ)若曲線C經(jīng)過伸縮變換![]() 后得到曲線C′,且直線l與曲線C′交于A,B兩點,求|MA|+|MB|.
后得到曲線C′,且直線l與曲線C′交于A,B兩點,求|MA|+|MB|.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com