
【題目】設全集U=R,集合A={x|-1≤x<3},B={x|2x-4≥x-2}.
(1)求U(A∩B);
(2)若集合C={x|2x+a>0},滿足B∪C=C,求實數a的取值范圍.
【答案】(1) U(A∩B)={x|x<2或x≥3}(2) a>-4.
【解析】試題分析:(1)求出集合B中不等式的解集確定出集合B,求出集合A與集合B的公共解集即為兩集合的交集,根據全集為R,求出交集的補集即可;
(2)求出集合C中的不等式的解集,確定出集合C,由B與C的并集為集合C,得到集合B為集合C的子集,即集合B包含于集合C,從而列出關于a的不等式,求出不等式的解集即可得到a的范圍.
解:(1)由集合B中的不等式2x﹣4≥x﹣2,解得x≥2,
∴B={x|x≥2},又A={x|﹣1≤x<3},
∴A∩B={x|2≤x<3},又全集U=R,
∴U(A∩B)={x|x<2或x≥3};
(2)由集合C中的不等式2x+a>0,解得x>﹣![]() ,
,
∴C={x|x>﹣![]() },
},
∵B∪C=C,
∴BC,
∴﹣![]() <2,解得a>﹣4;
<2,解得a>﹣4;
故a的取值范圍為(﹣4,+∞).


科目:高中數學 來源: 題型:
【題目】(本小題滿分12分)
甲乙兩個班級進行一門課程的考試,按照學生考試成績優秀和不優秀統計成績后,得到如下的列聯表:
班級與成績列聯表
優 秀 | 不優秀 | |
甲 班 | 10 | 35 |
乙 班 | 7 | 38 |
根據列聯表的獨立性檢驗,能否在犯錯誤的概率不超過0.01的前提下認為成績與班級有關系?
附:
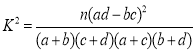
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設全集U=R,集合A={x|-1≤x<3},B={x|2x-4≥x-2}.
(1)求U(A∩B);
(2)若集合C={x|2x+a>0},滿足B∪C=C,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】類比平面內正三角形的“三邊相等,三內角相等”的性質,可推出正四面體的下列一些性質,你認為比較恰當的是( )
①各棱長相等,同一頂點上的任兩條棱的夾角都相等;②各個面都是全等的正三角形,相鄰兩個面所成的二面角都相等;③各個面都是全等的正三角形,同一頂點上的任兩條棱的夾角都相等。
A. ① B. ②③ C. ①② D. ①②③
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在各項都不相等的等差數列{an}中,a1,a2是關于x的方程x2-7a4x+18a3=0的兩個實根.
(1) 試判斷-22是否在數列{an}中;
(2) 求數列{an}的前n項和Sn的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的兩個焦點分別為
的兩個焦點分別為![]() ,離心率為
,離心率為![]() .設過點
.設過點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 相交于不同兩點
相交于不同兩點![]() ,
, ![]() 周長為
周長為![]() .
.
(Ⅰ)求橢圓C的標準方程;
(Ⅱ)已知點![]() ,證明:當直線
,證明:當直線![]() 變化時,總有TA與
變化時,總有TA與![]() 的斜率之和為定值.
的斜率之和為定值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com