
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
分析 按照給出的定義對四個命題結合數列的知識逐一進行判斷真假.對于①:列舉即可;對于②:需舉反例;對于③,可用數學歸納法加以證明;對于④:可由歸納推理判斷其正誤.
解答 解:對于①:當a=5時,x1=5,x2=$[\frac{5+[\frac{5}{5}]}{2}]$=3,x3=$[\frac{3+[\frac{5}{3}]}{2}]$=2,故①正確;
對于②:當a=1時,x2=$[\frac{1+[\frac{1}{1}]}{2}]$=1,x3=1,xk恒等于[$\sqrt{1}$]=1;
當a=2時,x1=2,x2=$[\frac{3+1}{2}]$=1,x3=$[\frac{1+[\frac{2}{1}]}{2}]$=1,
∴當k≥2時,恒有xk=[$\sqrt{2}$]=1;
當a=3時,x1=3,x2=2,x3=1,x4=2,x5=1,x6=2,x7=1,…,
此時數列{xn}除第一項外,從第二項起以后的項以2為周期重復出現,
因此不存在正整數k,使得n≥k時,總有xn=xk,故②不正確;
對于③:在xn+[$\frac{a}{{x}_{n}}$]中,當$\frac{a}{{x}_{n}}$為正整數時,xn+[$\frac{a}{{x}_{n}}$]=xn+$\frac{a}{{x}_{n}}$≥2$\sqrt{a}$,
∴xn+1=$[\frac{{x}_{n}+[\frac{a}{{x}_{n}}]}{2}]$≥[$\frac{2\sqrt{a}}{2}$]=[$\sqrt{a}$];
當$\frac{a}{{x}_{n}}$不是正整數時,令[$\frac{a}{{x}_{n}}$]=$\frac{a}{{x}_{n}}$-t,t為$\frac{a}{{x}_{n}}$的小數部分,
0<t<1,xn+1=$[\frac{{x}_{n}+[\frac{a}{{x}_{n}}]}{2}]$=$[\frac{{x}_{n}+[\frac{a}{{x}_{n}}]-t}{2}]$>[$\frac{2\sqrt{a}-t}{2}$]=[$\sqrt{a}$-$\frac{t}{2}$]=[$\sqrt{a}$],
∴xn+1≥[$\sqrt{a}$],∴xn≥[$\sqrt{a}$],∴xn>$\sqrt{a}$-1,故③正確;
由以上論證知,存在某個正整數k,若xk+1≥xk,
則當n≥k時,總有xn=[$\sqrt{a}$],故④正確.
故選:B
點評 本題主要考查了數列遞推公式的應用,歸納推理和演繹推理的方法,直接證明和間接證明方法,數學歸納法的應用,難度較大,需有較強的推理和思維能力.


 口算心算速算應用題系列答案
口算心算速算應用題系列答案 同步拓展閱讀系列答案
同步拓展閱讀系列答案科目:高中數學 來源: 題型:解答題
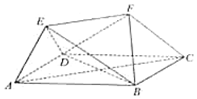 如圖,在多面體ABCDEF中,底面ABCD是菱形,AB=2,∠DAB=60°,EF∥AC,EF=$\sqrt{3}$.
如圖,在多面體ABCDEF中,底面ABCD是菱形,AB=2,∠DAB=60°,EF∥AC,EF=$\sqrt{3}$.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 6 | B. | 8 | C. | 9 | D. | 10 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
 如圖,在正方體ABCD-A1B1C1D1中,棱AB的中點為P,若光線從點P出發,依次經三個側面BCC1B1,DCC1D1,ADD1A1反射后,落到側面ABB1A1(不包括邊界),則入射光線PQ與側面BCC1B1所成角的正切值的范圍是( )
如圖,在正方體ABCD-A1B1C1D1中,棱AB的中點為P,若光線從點P出發,依次經三個側面BCC1B1,DCC1D1,ADD1A1反射后,落到側面ABB1A1(不包括邊界),則入射光線PQ與側面BCC1B1所成角的正切值的范圍是( )| A. | ($\frac{3}{4}$,$\frac{5}{4}$) | B. | ($\frac{2\sqrt{17}}{17}$,4) | C. | ($\frac{\sqrt{5}}{5}$,$\frac{3}{2}$) | D. | ($\frac{3\sqrt{5}}{10}$,$\frac{5}{4}$) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | f(π)<f(3)<f($\sqrt{2}$) | B. | f(π)<f($\sqrt{2}$)<f(3) | C. | f($\sqrt{2}$)<f(3)<f(π) | D. | f($\sqrt{2}$)<f(π)<f(3) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com