
 在x=1處連續,則
在x=1處連續,則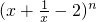 展開式中常數項是
展開式中常數項是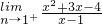 =5=n+(1)3,可得n的值,進而可得,(x+
=5=n+(1)3,可得n的值,進而可得,(x+ -2)4=(x+
-2)4=(x+ -2)•(x+
-2)•(x+ -2)•(x+
-2)•(x+ -2)•(x+
-2)•(x+ -2),其常數項必然是4個括號中,都取(-2);或兩個取x,剩下兩個取(
-2),其常數項必然是4個括號中,都取(-2);或兩個取x,剩下兩個取( );或兩個取(-2),剩下兩個一個取x,一個取(
);或兩個取(-2),剩下兩個一個取x,一個取( );分別求出其情況數目,由加法原理計算可得答案.
);分別求出其情況數目,由加法原理計算可得答案. 在x=1處連續,
在x=1處連續,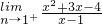 =5=n+(1)3,
=5=n+(1)3, -2)4=(x+
-2)4=(x+ -2)•(x+
-2)•(x+ -2)•(x+
-2)•(x+ -2)•(x+
-2)•(x+ -2),
-2), );或兩個取(-2),剩下兩個一個取x,一個取(
);或兩個取(-2),剩下兩個一個取x,一個取( );
);

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源:2010年江西省南昌市新建二中高考數學二模試卷(理科)(解析版) 題型:選擇題
 在x=1處連續,則
在x=1處連續,則 展開式中常數項是( )
展開式中常數項是( )查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com