
【題目】已知橢圓![]() 的左焦點為
的左焦點為![]() 且經過點
且經過點![]() 分別是
分別是![]() 的右頂點和上頂點,過原點
的右頂點和上頂點,過原點![]() 的直線
的直線![]() 與
與![]() 交于
交于![]() 兩點(點
兩點(點![]() 在第一象限),且與線段
在第一象限),且與線段![]() 交于點
交于點![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)若![]() ,求直線
,求直線![]() 的方程;
的方程;
(3)若![]() 的面積是
的面積是![]() 的面積的
的面積的![]() 倍,求直線
倍,求直線![]() 的方程.
的方程.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)利用橢圓的定義即可求出![]() 的值,從而求出
的值,從而求出![]() ,從而得到答案.
,從而得到答案.
(2)根據題意設出直線方程,聯立方程由根與系數的關系可得![]() ,再利用弦長公式即可得到答案.
,再利用弦長公式即可得到答案.
(3)依題設出點![]() 的坐標以及直線
的坐標以及直線![]() 的斜率,根據題目條件即可得坐標之間的關系,從而求出直線
的斜率,根據題目條件即可得坐標之間的關系,從而求出直線![]() 的斜率,從而求出直線直線
的斜率,從而求出直線直線![]() 的方程.
的方程.
(1)依題知![]() 則橢圓的右焦點為
則橢圓的右焦點為![]() ,
,
因為點![]() 在橢圓上,且
在橢圓上,且![]() ,
,
又![]() ,所以
,所以![]() ,所以
,所以![]()
所以![]() ,
,
所以橢圓的標準方程為![]() .
.
(2)因為點![]() 在第一象限,所以直線
在第一象限,所以直線![]() 的斜率存在,
的斜率存在,
設直線![]() 的斜率為
的斜率為![]() ,則直線
,則直線![]() 的方程為
的方程為![]() ,
,
設直線 ![]() 與該橢圓的交點為
與該橢圓的交點為![]() ,
,
由![]() 可得
可得![]() ,
,
易知![]() ,且
,且![]() ,
,
則![]()
![]() ,所以
,所以![]() ,
,
又![]() ,所以直線
,所以直線![]() 的方程為
的方程為![]() .
.
(3)設![]() ,
,![]() ,則
,則![]() ,
,
易知![]() ,
,![]() .由
.由![]() ,
,![]() ,
,
所以直線![]() 的方程為
的方程為![]() ,即
,即![]() .
.
若![]() 的面積是
的面積是![]() 的面積的4倍,
的面積的4倍,
則![]() ,由
,由![]() 關于原點對稱,可得
關于原點對稱,可得![]() ,
,
所以![]() ,所以
,所以![]() 即
即![]() ① .
① .
設直線![]() 的方程為
的方程為![]() ,
,
由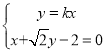 得
得![]() ,
,
由![]() 得
得![]() ,
,
代入①可得![]()
![]() ,
,
化簡得![]() ,解得
,解得![]() ,
,
所以直線![]() 的方程為:
的方程為:![]() .
.


 新課標快樂提優暑假作業陜西旅游出版社系列答案
新課標快樂提優暑假作業陜西旅游出版社系列答案 暑假銜接培優教材浙江工商大學出版社系列答案
暑假銜接培優教材浙江工商大學出版社系列答案 欣語文化快樂暑假沈陽出版社系列答案
欣語文化快樂暑假沈陽出版社系列答案科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程
的參數方程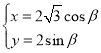 (
(![]() 為參數).直線
為參數).直線![]() 的參數方程
的參數方程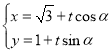 (
(![]() 為參數).
為參數).
(Ⅰ)求曲線![]() 在直角坐標系中的普通方程;
在直角坐標系中的普通方程;
(Ⅱ)以坐標原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系,當曲線
軸的正半軸為極軸建立極坐標系,當曲線![]() 截直線
截直線![]() 所得線段的中點極坐標為
所得線段的中點極坐標為![]() 時,求直線
時,求直線![]() 的傾斜角.
的傾斜角.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x-1+![]() (a∈R,e為自然對數的底數).且曲線y=f(x)在點(1,f(1))處的切線平行于x軸.
(a∈R,e為自然對數的底數).且曲線y=f(x)在點(1,f(1))處的切線平行于x軸.
(1)求a的值;
(2)求函數f(x)的極值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】由我國引領的5G時代已經到來,5G的發展將直接帶動包括運營、制造、服務在內的通信行業整體的快速發展,進而對![]() 增長產生直接貢獻,并通過產業間的關聯效應和波及效應,間接帶動國民經濟各行業的發展,創造岀更多的經濟增加值.如圖是某單位結合近年數據,對今后幾年的5G經濟產出所做的預測.結合下圖,下列說法正確的是( )
增長產生直接貢獻,并通過產業間的關聯效應和波及效應,間接帶動國民經濟各行業的發展,創造岀更多的經濟增加值.如圖是某單位結合近年數據,對今后幾年的5G經濟產出所做的預測.結合下圖,下列說法正確的是( )
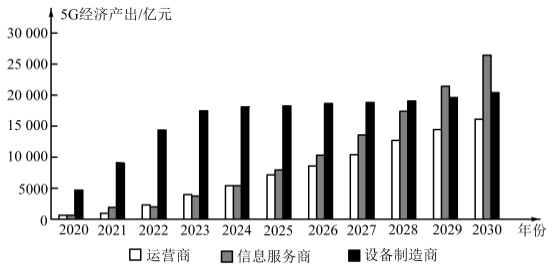
A.5G的發展帶動今后幾年的總經濟產出逐年增加
B.設備制造商的經濟產出前期增長較快,后期放緩
C.設備制造商在各年的總經濟產出中一直處于領先地位
D.信息服務商與運營商的經濟產出的差距有逐步拉大的趨勢
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】把函數![]() 的圖象向右平移一個單位,所得圖象與函數
的圖象向右平移一個單位,所得圖象與函數![]() 的圖象關于直線
的圖象關于直線![]() 對稱;已知偶函數
對稱;已知偶函數![]() 滿足
滿足![]() ,當
,當![]() 時,
時,![]() ;若函數
;若函數![]() 有五個零點,則
有五個零點,則![]() 的取值范圍是( )
的取值范圍是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】等差數列{an}的前n項和為Sn,且![]() =9,S6=60.
=9,S6=60.
(I)求數列{an}的通項公式;
(II)若數列{bn}滿足bn+1﹣bn=![]() (n∈N+)且b1=3,求數列
(n∈N+)且b1=3,求數列![]() 的前n項和Tn.
的前n項和Tn.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠有兩種日工資方案供員工選擇,方案一規定每日底薪50元,計件工資每件3元;方案二規定每日底薪100元,若生產的產品數不超過44則沒有計件工資,若超過則從第45件開始,計件工資每件5元.該工廠隨機抽取100天的工人生產量的數據.將樣本數據分為![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 七組,整理得到如圖所示的頻率分布直方圖.
七組,整理得到如圖所示的頻率分布直方圖.
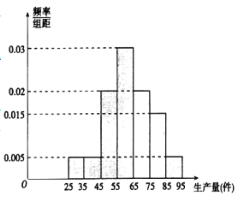
(1)隨機選取一天,估計這一天該工廠的人均生產量不少于65件的概率;
(2)若甲、乙選擇了日工資方案一,丙、丁選擇了日工資方案二.現從上述4名工人中隨機選取2人.求至少有1名工人選擇方案一的概率;
(3)若僅從人均日收入的角度考慮,請你利用所學的統計學知識為新聘工人做出日工資方案的選擇,并說明理由.(同組中的每個數據用該組區間的中點值代替)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分12分)某商場為了了解顧客的購物信息,隨機的在商場收集了100位顧客購物的相關數據,整理如下:
一次購物款(單位:元) | [0,50) | [50,100) | [100,150) | [150,200) | [200,+∞) |
顧客人數 | m | 20 | 30 | n | 10 |
統計結果顯示100位顧客中購物款不低于100元的顧客占60%,據統計該商場每日大約有5000名顧客,為了增加商場銷售額度,對一次性購物不低于100元的顧客發放紀念品(每人一件).(注:視頻率為概率)
(1)試確定![]() 的值,并估計該商場每日應準備紀念品的數量;
的值,并估計該商場每日應準備紀念品的數量;
(2)為了迎接店慶,商場進行讓利活動,一次購物款200元及以上的一次返利30元;一次性購物
款小于200元的按購物款的百分比返利,具體見下表:
一次購物款(單位:元) | [0,50) | [50,100) | [100,150) | [150,200) |
返利百分比 | 0 | 6% | 8% | 10% |
估計該商場日均讓利多少元?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com